算法第一章 动态规划
一、动态规划的思想
动态规划的核心思想是通过寻找子问题的最优解来构造原问题的最优解。在应用动态规划的过程中,需要找到问题的状态转移方程,并利用储存中间结果的方法来避免重复计算。
总的来说,动态规划的思想包括:分析问题具有的重叠子问题性质、定义子问题的递推关系、储存中间结果以避免重复计算、推导出问题的最优解。二、动态规划五要素
- 最优子结构
- 重叠子问题
- 状态转移方程
- 边界条件
- 填表法
解题思路
这里以抖音-最短编辑距离为例题,讲解动态规划的思路

构建问题: 输入两个字符串,返回最小编辑距离,用函数
Question(word1,word2) = minEditDist来抽象分解子问题: 一个大的问题可以拆成若干子问题,例如
Qusetion(word,word)就是一个更小的子问题,Qusetion("","")就是最小的子问题,把所有的子问题列出来,形成二维矩阵,状态(i,j)表示 word1 前 i 个字符变成 word2 前 j 个字符的最小操作

- 求解简单子问题,最基本的子问题一般可以直接推导
dp("","") = 0,两个空串不用编辑,直接相等dp(0,j) = j, 将空串变成字符串 j,显然添加 j 个字符后相等dp(i,0) = i, 将字符串 i 变成空串,显然删除 i 个字符后相等

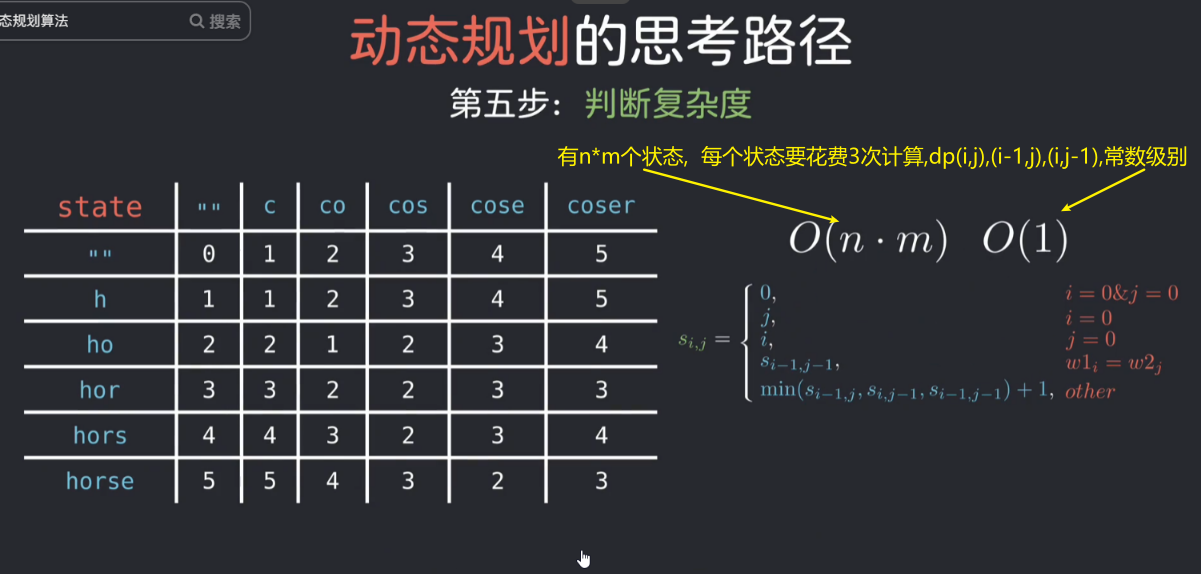
- 通过已知问题求解,现在通过填表法,
dp(i-1,j-1)和dp(i,j-1)和dp(i-1,j)已经算出,例如图中的Question(c,h),所以可以采用从左到右,从上到下的填表法
所以,dp[i][j]等于dp(i-1,j-1)和dp(i,j-1)和dp(i-1,j)的最小值+1


- 计算时间复杂度
最终代码
/* 72. 编辑距离
中等
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
提示:
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成 */
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
int dp[501][501];
int minEditDist(string a, string b)
{
int len_a = a.size();
int len_b = b.size();
a = '#' + a;
b = '@' + b;
// int dp[len_a + 1][len_b + 1];
for (int i = 0; i <= len_a; i++)
{
for (int j = 0; j <= len_b; j++)
{
if (i == 0 && j == 0)
{
dp[i][j] = 0;
}
else if (i == 0)
dp[i][j] = j;
else if (j == 0)
dp[i][j] = i;
else if (a[i] == b[j])
{
dp[i][j] = dp[i - 1][j - 1];
}
else
{
dp[i][j] = min(min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
}
}
}
return dp[len_a][len_b];
}
int test01()
{
string a, b;
cin >> a >> b;
cout << "结果是" << minEditDist(a, b);
return 0;
}三、例题
矩阵相乘问题
矩阵相乘问题
这道题的关键在于矩阵乘法的次数和举证的行列数有关,2行3列的矩阵乘3行4列的矩阵要乘2*4次解法1:
#include <iostream>
#include <climits>
using namespace std;
int main() {
int n;
cin >> n; // 输入矩阵个数
int m[n+1][n+1]; // 定义子问题数组 m[i][j] 表示第 i 个矩阵到第 j 个矩阵的最少乘次数
int p[n+1]; // n 个矩阵乘法要有 n+1 个行列数据
for (int i = 0; i <= n; i++) {
cin >> p[i];
}
for (int i = 1; i <= n; i++) {
m[i][i] = 0; // 初始化对角线元素为 0
}
for (int l = 2; l <= n; l++) {
for (int i = 1; i <= n - l + 1; i++) {
int j = i + l - 1;
m[i][j] = INT_MAX;
for (int k = i; k <= j - 1; k++) {
int temp = m[i][k] + m[k+1][j] + p[i-1] * p[k] * p[j];
if (temp < m[i][j]) {
m[i][j] = temp;
}
}
}
}
cout << m[1][n];
return 0;
}解法2:
//状态转移方程 : dp[i][j] = min(dp[i][k] + dp[k+1][j] + p[i-1] * p[k] * p[j]) (i < k < j)
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int n;//矩阵的个数
cin >> n;
int** dp = new int* [n + 1]; // 分配n+1个指向整数数组的指针,dp数组表示从第i个矩阵乘到第j个矩阵
for (int i = 0; i < n + 1; i++) {
dp[i] = new int[n + 1]; // 为每个指针分配整数数组
}
int *p = new int [n+1];//行列数据
// 对数组进行赋值
for (int i = 0; i <= n; i++) {
cin >> p[i];
}
//边界条件或初始化
for (int i = 1; i <= n; i++) {
dp[i][i] = 0; //自身不用乘,把对角线置为0
}
for (int i = n; i >= 1; i--) {//从下往上,自左而右的填表 dp[i][j]必须要知道左侧的和下方的dp解
for (int j = i+1; j <= n; j++) {
dp[i][j] = INT_MAX; //初始化为一个最大的值
for (int k = i; k <= j-1; k++) {
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + p[i - 1] * p[k] * p[j]);
}
}
}
for (int i = 0; i <= n; i++) {
for (int j = i; j <= n; j++) {
cout << "dp[" << i << "][" << j << "]" << dp[i][j] << endl;
}
}
cout << dp[1][n] <<endl;
for (int i = 0; i < n + 1; i++) {
delete[] dp[i]; // 释放每个数组
}
delete[] dp; // 释放指针数组
return 0;
}最大子段和问题
最大子段和问题
/*
给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给整数均为负数时,定义子段和为0。
要求算法的时间复杂度为O(n)。
输入格式:
输入有两行:
第一行是n值(1<=n<=10000);
第二行是n个整数。
输出格式:
输出最大子段和。
输入样例:
在这里给出一组输入。例如:
6
-2 11 -4 13 -5 -2
输出样例:
在这里给出相应的输出。例如:
20
*/
//状态转移方程dp[i] = max(dp[i-1] + nums[i],nums[i]); //字段的定义是连续的,所以dp[i]只可能接着上一段或者当前数字开头做新一段
#include <iostream>
#include <cstring>
using namespace std;
int MaxSum = 0;
int getMaxSum(int arr[], int dp[], int n) {
int count = 0;
dp[0] = arr[0];
for (int i = 0; i < n; i++) {
if (arr[i] < 0) {
count++;
}
}
if (count == n) {
MaxSum = 0;
}
else {
for (int i = 1; i < n; i++) {
dp[i] = max(dp[i - 1] + arr[i], arr[i]);
MaxSum = max(MaxSum, dp[i]);
}
}
return MaxSum;
}
int main(){
int n;
cin >> n;
int* nums = new int[n];
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
int* dp = new int[n];//从第个数到第n个数的最大子段和
memset(dp, 0, sizeof dp);
int result = getMaxSum(nums, dp, n);
cout << result << endl;
return 0;
}0-1 背包问题
0-1背包问题
/*
7-20 0-1背包
给定n(n<=100)种物品和一个背包。物品i的重量是wi(wi<=100),价值为vi(vi<=100),背包的容量为C(C<=1000)。
应如何选择装入背包中的物品,使得装入背包中物品的总价值最大? 在选择装入背包的物品时,对每种物品i只有两个选择:装入或装入。不能将物品i装入多次,也不能只装入部分物品i。
输入格式:
共有n+1行输入:
第一行为n值和c值,表示n件物品和背包容量c;
接下来的n行,每行有两个数据,分别表示第i(1≤i≤n)件物品的重量和价值。
输出格式:
输出装入背包中物品的最大总价值。
输入样例:
在这里给出一组输入。例如:
5 10
2 6
2 3
6 5
5 4
4 6
输出样例:
在这里给出相应的输出。例如:
15
*/
//状态转移方程: if (j >= weights[i]) {
//dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i]] + values[i]);
// }
// else {
// dp[i][j] = dp[i - 1][j];
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int n, c;
cin >> n >> c;
int weights[31];
int values[31]; //多定义一个空间,让第i件物品价值对应
for (int i = 1; i <= n; i++) {
cin >> weights[i] >> values[i];
}
int dp[31][1001] = { 0 };
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= c; j++) {
if (j >= weights[i]) {
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i]] + values[i]);
}
else {
dp[i][j] = dp[i - 1][j];
}
}
}
//输出最优解
int x = n;
int y = c;
while(x > 0 && y>0){
if(dp[x-1][y] != dp[x][y]){
cout << x << " ";
y-=weights[x];
}x--;
}
cout << dp[n][c] << endl;
return 0;
}子集和
子集和
/*
7-2 子集和
给定n个不同的整数的集合,求有多少个子集的和为m
输入格式:
第一行两个数字n(0<n<=100)和m(0<m<=5000),以空格分隔
第二行n个不同的整数,以空格分隔
输出格式:
和为m的子集的个数
输入样例:
5 6
1 2 3 4 5
输出样例:
3
*/
/*
状态转移方程:
dp[i][j] = dp[i + 1][j];
if (j >= nums[i - 1]) {
dp[i][j] += dp[i + 1][j - nums[i - 1]];
}
*/
#include <iostream>
#include <stdio.h>
using namespace std;
#define MAX 5000
int dp[MAX][MAX];//dp[i][j]表示第i个数开始到结尾,剩余和为j的最优解
int nums[MAX];
int n, m;
int solve() {
for (int i = 1; i <= m; i++) {
dp[n][i] = 0;//第n个数开始到结尾即第i个数和为任何数的子集数为0
}
dp[n][0] = 1;
if (m >= nums[n]) {
dp[n][nums[n]] = 1;
}
for (int i = n - 1; i >= 1; i--) {
for (int j = 0; j <= m; j++) {
dp[i][j] = dp[i + 1][j];
if (j >= nums[i]) {
dp[i][j] += dp[i + 1][j - nums[i]];
}
}
}
return dp[1][m];
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> nums[i];
}
cout << solve() << endl;
return 0;
}最长公共子序列问题
最长公共子序列问题
#include <iostream>
#include <string>
using namespace std;
int dp[105][105]; //表示长度为i和j的最长公共子序列长度
string A, B;
int alen;
int blen;
int LCSlength() {
// 0, A == 0 || B == 0
for (int i = 0; i <= alen; i++) {
dp[i][0] = 0;
}
for (int i = 0; i <= blen; i++) {
dp[0][i] = 0;
}
for (int i = 1; i <= alen; i++) {
for (int j = 1; j <= blen; j++) {
if (A[i-1] == B[j-1]) { // previously incorrect line: A[i] -> A[i-1]
dp[i][j] = dp[i-1][j-1] + 1;
} else if (dp[i][j-1] > dp[i-1][j]) {
dp[i][j] = dp[i][j - 1];
} else {
dp[i][j] = dp[i-1][j];
}
}
}
return dp[alen][blen];
}
void printLCS(int alen, int blen){
if(alen == 0 || blen ==0){
return;
}else if(x[alen -1] == y[blen -1]){
printLCS(alen-1,blne-1);
cout << x[alen-1];
}else if(c[alen-1][blne] > c[alne][blen-1]){
printLCS(alne-1,blen);
}else{
printLCS(alen,blen-1);
}
}
int main() {
cin >> A >> B;
alen = A.length();
blen = B.length();
int l = LCSlength();
cout << l << endl; // previously incorrect line: << result << endl -> << endl.
printLCS(alen,blen);
return 0; // main function should return a value
}算法第二章 分治法
一、分治法的思想
分治法就是不断的划分子问题,直到子问题的规模足够小到可以直接求解,再通过合并子问题求得原来的子问题的解二、分治法的时间复杂度
三、分治法之排序问题
快速排序
快速排序
#include <iostream>
#include <algorithm>
using namespace std;
int partition(int arr[], int left, int right) {
int pivot = arr[left];
int i = left + 1;
int j = right;
while (i <= j) {
while (i <= right && arr[i] < pivot) {
i++;
}
while (j >= left + 1 && arr[j] > pivot) {
j--;
}
if (i <= j) {
swap(arr[i], arr[j]);
i++;
j--;
}
}
swap(arr[left], arr[j]);
return j;
}
void quickSort(int arr[], int left, int right) {
if (left >= right) {
return;
}
int pivotIndex = partition(arr, left, right);
quickSort(arr, left, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, right);
}
int main() {
int n;
cout << "Enter the size of the array: ";
cin >> n;
if (n <= 0) {
cout << "Invalid array size." << endl;
return 0;
}
int* nums = new int[n];
cout << "Enter the elements of the array: ";
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
quickSort(nums, 0, n - 1);
cout << "Sorted array: ";
for (int i = 0; i < n; i++) {
cout << nums[i] << " ";
}
cout << endl;
delete[] nums;
return 0;
}归并排序
归并排序
#include <iostream>
using namespace std;
void Merge(int arr[], int temp[], int left, int right, int mid) {
int i = left;
int j = mid + 1;
int k = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
}
else {
temp[k++] = arr[j++];
}
}
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= right) {
temp[k++] = arr[j++];
}
for (int i = 0; i < k; i++) {
arr[left + i] = temp[i];
}
}
void MergeSort(int arr[], int left, int right) {
if (left >= right) {
return;
}
int mid = left + (right - left) / 2;
MergeSort(arr, left, mid);
MergeSort(arr, mid + 1, right);
int* temp = new int[right - left + 1];
Merge(arr, temp, left, right, mid);
delete[] temp;
}
int main() {
int n;
cin >> n;
int* nums = new int[n];
int num;
for (int i = 0; i < n; i++) {
cin >> num;
nums[i] = num;
}
MergeSort(nums, 0, n - 1);
for (int i = 0; i < n; i++) {
cout << nums[i] << " ";
}
delete[] nums;
return 0;
}四、分治法之查找问题
二分查找(递归)
二分搜索
/*
给定已按降序排好的n个元素a[0:n-1],在这n个元素中找出一特定元素x。
输入格式:
第一行为n值(n<=10^6)和查询次数m(m<=10^3);
第二行为n个整数。
接下来m个数,代表要查询的x
输出格式:
对于每一个查询的x,如果找到,输出x的下标;否则输出-1。
输入样例:
5 2
5 4 3 2 1
3
6
输出样例:
2
-1
*/
#include <iostream>
#include <algorithm>
using namespace std;
int binarySearch(int arrs[], int left, int right, int tag) {//参数传入搜索范围就不用每次while循环更改mid值
/*否则如果这样回传搜索范围就要更新
int left = 0;
int right = n;
int mid = left + (right - left) / 2;
*/
if (left > right) {
return -1; // 未找到
}
int mid = left + (right - left) / 2;
if (arrs[mid] == tag) {
return mid; // 找到目标元素,返回索引
}
if (tag < arrs[mid]) {
return binarySearch(arrs, left, mid - 1, tag); // 递归搜索左半部分
}
if (tag > arrs[mid]) {
return binarySearch(arrs, mid + 1, right, tag); // 递归搜索右半部分
}
}
int main() {
int n, m;
cin >> n >> m;
int nums[n];
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
int tags[m];
for (int i = 0; i < m; i++) {
cin >> tags[i];
}
int result[m];
// 使用二分查找前,先保证数组是排好序的
sort(nums, nums + n);//升序排列
for (int i = 0; i < m; i++) {
result[i] = binarySearch(nums, 0, n - 1, tags[i]);
}
for (int i = 0; i < m; i++) {
cout << result[i] << endl;
}
return 0;
}
二分查找基础版(迭代)
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; //注意数组的范围
int mid = (left + right) / 2;
while(left<=right){
if(nums[mid] == target){
return mid;
}else if(nums[mid] > target){
right = mid - 1; //注意查找的范围,既然不等,就不用把mid包含进去
}else{
left = mid + 1;
}
mid = (left + right) / 2;
}
return -1;
}
};二分搜索返回数组(指针)
//在 C++ 中,函数不能直接返回数组。你可以使用指针或者容器来表示数组。在你的情况下,你可以返回一个 `int*` 指针来表示数组。这个指针指向动态分配的内存,可以在函数外部进行释放。
//另外,C++17 引入了 `std::array` 和 `std::vector` 这样的标准库容器,它们可以更方便地表示数组,并且具有更好的安全性和易用性。你可以考虑使用它们来代替裸指针。
//下面是使用 `int*` 指针表示数组的代码:
#include <iostream>
using namespace std;
int* binarySearch(int arr[], int target, int left, int right) {
int* result = new int[2];
int middle;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
result[0] = mid;
result[1] = mid;
return result;
}
if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
middle = mid;
}
// 目标值未找到
result[0] = middle;//result[0] = right;
result[1] = middle;//result[1] = left;
return result;
}
int main() {
int n, x;
cin >> n >> x;
int* data = new int[n];
for (int i = 0; i < n; i++) {
cin >> data[i];
}
if (x < data[0]) {
cout << -1 << " " << 0 << endl;
delete[] data;
return 0;
}
if (x > data[n - 1]) {
cout << n - 1 << " " << n << endl;
delete[] data;
return 0;
}
int* num = binarySearch(data, x, 0, n - 1);
cout << num[0] << " " << num[1] << endl;
delete[] data;
delete[] num;
return 0;
}
//希望这可以帮助你理解如何在 C++ 中返回数组。算法第三章 贪心算法
一、贪心算法的思想
贪心算法:在每一次选择中选择当前情况的最优解,达到整体问题的最优解
值得注意的是,贪心问题必须满足
1.贪心选择性质
贪心选择性质指的是,通过贪心策略所做出的每一个局部最优的选择,都能够组合成一个全局最优解。换句话说
就是贪心算法每次选择的都是当前状态下最优的策略,而这些最优的策略组合在一起,可以形成最终的最优解。
2.最优子问题
最优子结构指的是,问题的最优解可以通过子问题的最优解构建出来,换句话说,问题可以被分解成更小的子问题,子问题的最优解可以构成原问题的最优解。这个性质是动态规划和贪心算法设计的前提之一。
二、例题
完全背包问题
完全背包问题
/*
7-35 背包问题
分数 25
作者 郑琪
单位 广东外语外贸大学
给定n(n<=100)种物品和一个背包。物品i的重量是wi,价值为vi,背包的容量为C(C<=1000)。问:应如何选择装入背包中的物品,使得装入背包中物品的总价值最大? 装入背包的物品可以只装入部分物品。
输入格式:
共有n+1行输入: 第一行为n值和c值,表示n件物品和背包容量c; 接下来的n行,每行有两个数据,分别表示第i(1≤i≤n)件物品的重量和价值。
输出格式:
输出装入背包中物品的最大总价值。
输入样例:
5 10
2 6
2 3
6 5
5 4
4 6
输出样例:
16.67
*/
#include <algorithm>
#include <iostream>
using namespace std;
struct Goods {
double weight;
double value;
}goods[105];
bool cmp(Goods a, Goods b) {
if (a.value / a.weight > b.value / b.weight)
return true;
else
return false;
}
int main() {
int n;
double c; //背包容量
cin >> n >> c;
for (int i = 0; i < n; i++) {
cin >> goods[i].weight >> goods[i].value;
}
sort(goods, goods + n, cmp);
double VALUE = 0;
int i = 0;
while (c > 0 && i < n) {
if (c >= goods[i].weight) {
VALUE += goods[i].value;
c -= goods[i].weight;
i++;
}
else {
VALUE += c * (goods[i].value / goods[i].weight);
break;
}
}
printf("%.2f\n", VALUE);
return 0;
}迪杰斯特拉算法
#include <bits/stdc++.h>
#define MAX 11
using namespace std;
int t[MAX][MAX]; //邻接矩阵 表示一个地点到另一个地点花费的时间
int s[MAX]; //经过点的集合 赋值为1则在集合中 赋值为0则不在集合中
int dist[MAX];//特定地点到各个点的最短时间
int main(){
int i;
int N, M, D;//D代表有向无向
cin >> N >> M >> D;
memset(t, 0x3f3f3f, sizeof t);//给每个邻接矩阵赋很大的值
for(i = 1; i <= M; i++){
int v, u, w;
cin >> v >> u >> w;
t[v][u] = w;
if(!D)//如果是无向图,返过来也要赋值
t[u][v] = w;
}
memset(s, 0, sizeof s);//集合置为空
int sourse;//原点
cin >> sourse;
s[sourse] = 1;
//memset(dist, 0x3f, sizeof s);
for(i = 1; i <= N; i++)
dist[i] = t[sourse][i];
dist[sourse] = 0;
for(int k = 1; k <= N; k++){
int minv = 0x3f3f3f;
int mini;
for(i = 1; i <= N; i++){
if(s[i] == 0 && dist[i] < minv){//不在集合中
mini = i;
minv = dist[i];
}
}
s[mini] = 1;
for(i = 1; i <= N; i++)
dist[i] = min(dist[i], dist[mini] + t[mini][i]);
}
for(i = 1; i <= N; i++){
cout << sourse << "->" << i << ":";
if(dist[i] < 0x3f3f3f)
cout << dist[i] << endl;
else
cout << "no path" << endl;
}
return 0;
}算法第五章 回溯法(深度优先)
1.回溯法的思想
有许多问题,当需要找出它的解集或者要求回答什么解是满足某些约束条件的最佳解时,往往要使用回溯法。
回溯法的基本做法是搜索,或是一种组织得井井有条的,能避免不必要搜索的穷举式搜索法。这种方法适用于解一些组合数相当大的问题。
回溯法在问题的解空间树中,按深度优先策略,从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时,先判断该结点是否包含问题的解。如果肯定不包含,则跳过对该结点为根子树的搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先策略搜索。
若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。 而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。解空间
1、问题的解空间 复杂问题常常有很多的可能解,这些可能解构成了问题的解空间。解空间也就是进行穷举的搜索空间,所以,解空间中应该包括所有的可能解。确定正确的解空间很重要,如果没有确定正确的解空间就开始搜索,可能会增加很多重复解,或者根本就搜索不到正确的解。 例如,对于有n个物品的0/1背包问题,当n=3时,其解空间是: {(0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0), (1, 1, 1) }基本步骤
剪枝函数
常用剪枝函数: 用约束函数在扩展结点处剪去不满足约束的子树; 用限界函数剪去得不到最优解的子树;
子集树和排列树
- 子集树:当所给的问题是从 n 个元素的集合 S 中找出满足某种性质的子集时,相应的解空间树成为子集树。例:0-1 背包问题。
- 排列树:当所给问题是确定 n 个元素的满足排列树:当所给问题是确定 n 个元素的满足某种性质的排列时,相应的解空间树称为排列树。例:旅行售货员问题。
2. 例题
迷宫问题
迷宫问题:给你一个而且只有一个出口的迷宫,你需要从入口出发,穿过迷宫,走到出口。要求找到最短路径。
#include <iostream>
#include <vector>
using namespace std;
// 给你二维矩阵,零代表可以走,一代表不可以走,从起点到终点,计算一下最短路径
// 思路:DFS
vector<string> path = {};
vector<string> min_path = {};
vector<tuple<int, int, char>> directions = {{0, 1, 'R'}, {1, 0, 'D'}, {0, -1, 'L'}, {-1, 0, 'U'}};
int start_x, start_y, end_x, end_y;
int min_length = INT_MAX;
// 检查坐标是否在矩阵内,是返回true,否则返回false
bool check(int x, int y, int w, int h)
{
if (x < 0 || x >= w || y < 0 || y >= h)
{
return false;
}
return true;
}
void printPath()
{
cout << "最短路径:" << endl;
for (auto p : min_path)
{
cout << p << " ";
}
}
void dfs(vector<vector<int>> &matrix, int w, int h, int x, int y, int current_length)
{
// 不能走到边界或者已经访问过
if (!check(x, y, w, h) || matrix[x][y] == 1)
{
return;
}
if (x == end_x && y == end_y)
{
if (current_length < min_length)
{
min_length = current_length;
min_path = path;
}
return;
}
matrix[x][y] = 1; // 标记为已访问
for (auto [dx, dy, direction] : directions)
{
int nx = x + dx, ny = y + dy;
path.push_back(string(1, direction));
dfs(matrix, w, h, nx, ny, current_length + 1);
path.pop_back();
}
matrix[x][y] = 0; // 回溯,标记为未访问
}
int test01()
{
int w, h;
cin >> w >> h;
// 读入矩阵
vector<vector<int>> matrix(h, vector<int>(w));
for (int i = 0; i < h; i++)
{
for (int j = 0; j < w; j++)
{
cin >> matrix[i][j];
}
}
cin >> start_x >> start_y >> end_x >> end_y;
// 开始DFS
dfs(matrix, w, h, start_x, start_y, 0);
if (min_length != INT_MAX)
{
cout << "找到终点" << endl;
cout << "最短路径长度为:" << min_length << endl;
}
else
{
cout << "没有找到终点" << endl;
}
printPath();
return 0;
}0-1 背包
#include <iostream>
#include <algorithm>
using namespace std;
const int MAX = 100;
int result[MAX]; //最优解
int x[MAX];//当前节点的路径
double maxV;//最优解值
double cr;//剩余容量
double cv = 0;//当前价值
int n, c;//n个物品, 背包容量c
struct Good{
int index;
double weight;
double value;
}goods[MAX];
bool cmp(Good a,Good b) {
return a.value / a.weight > b.value / b.weight;
}
/*int bound(int t) {
double temp = cv;
for (int i = t + 1; i <= n; i++) {
cv += goods[i].value;
}
cv = temp;
return cv;
}*/
//限界函数
double bound(int i) {
double cleft = cr;
double b = cv;
while (i <= n && goods[i].weight < cleft) {
b += goods[i].value;
cleft -= goods[i].weight;
i++;
}
if (i <= n) {
b += goods[i].value * cleft / goods[i].weight;
}
return b;
}
void Backtrack(int t)
{//以深度优先的方式遍历第t层中的某棵子树(第t层就是选第t个物品)
if (t > n) { //遍历到叶子节点了
if (cv > maxV) {
maxV = cv;
for (int i = 1; i <= n; i++) {
result[i] = x[i];
}
}
return;
}
if (cr >= goods[t].weight)//该点选择物品时
{
cr -= goods[t].weight;
cv += goods[t].value;
x[t] = 1;
Backtrack(t + 1);//遍历完当前节点子树,回到父节点状态
cr += goods[t].weight;
cv -= goods[t].value;
}
//如果满足限界条件进入右子树
if (bound(t + 1) > maxV) {
x[t] = 0;
Backtrack(t + 1);
}
}
int main() {
cin >> n >> c;
for (int i = 1; i <= n; i++) {
cin >> goods[i].weight >> goods[i].value;
goods[i].index = i;
}
cr = c;
sort(goods + 1, goods + 1 + n, cmp);
//左不选0 右选1
Backtrack(1);
cout << maxV << endl;
cout << endl;
for (int i = 1; i <= n; i++) {
printf("第%d个物品%d\n", goods[i].index, result[i]);
}
}
//二叉树
//叶子节点有2n个, 节点有2^n-1个
//算法时间复杂度为O(2^n)子集和(子集树)
子集和问题(找到序列中子集和为v并输出)
#include <iostream>
using namespace std;
const int MAX = 1000;
int n,v; //数目 子集和
int a[MAX];//数据数组
int ans[MAX];//解集
int cv; //剩余价值
bool flag;//找到解标志记1
void Backsearch(int t) {
if(cv == 0) flag = 1;//剩余价值为0
if(t>n || flag == 1) return;//遍历到叶子节点或者找到解就结束这次回溯
if(flag == 0 && a[t] <= cv) {//未找到解且能装下当前带选择数
cv -= a[t];
ans[t] = a[t];
Backsearch(t+1);//向下遍历,没找到解才回归父节点状态
if(flag==0) cv += a[t];
if(flag==0) ans[t] = 0;
}
if(flag==0) { // 装不下,遍历右子树
Backsearch(t+1);
}
}
int main() {
cin >> n >> v;
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
flag = 0;
cv = v;//初始化剩余价值
Backsearch(1);
if(flag == 1) {
for(int i = 1; i <= n; i++) {
if(ans[i] != 0)
cout<< ans[i] <<" ";//输出解
}
} else
cout<<"No Solution!";
return 0;
}居民部落问题
#include <iostream>
using namespace std;
int R[201][201] = {0}; //关系矩阵
int x[201] = {0}, cx[201] = {0}; //x[i]=1表示居民在卫队中,反之不在
int n, m; //n是人数,m是仇敌关系数量
int max_num = 0, cmax = 0; //卫队中居民人数
bool Bound(int t1) //约束函数:当前的居民在卫队中中是否有仇敌关系
{
int j;
for (j=1; j<t1; j++)
{
if (cx[j]==1 && R[t1][j]==1)
{
return false;
}
}
return true;
}
void Back(int t)
{
if (t>n)
{
if (max_num < cmax)
{
max_num = cmax;
for (int i=1; i<=n; i++)
{
x[i] = cx[i];
}
}
return;
}
//1
if (Bound(t) == true) //当前居民在卫队中没有找到仇人
{
cx[t] = 1;
cmax++;
Back(t+1);
cmax--;
cx[t] = 0;
}
//0
if (cmax+n-t >= max_num) //剪枝:再往下找,考虑理想情况,卫队居民人数也不可能比当前最大的多了
{
Back(t+1);
}
}
int main()
{
int u, v;
cin >> n >> m;
for (int i=1; i<=m; i++)
{
cin >> u >> v;
R[u][v] = 1; R[v][u] = 1; //对称矩阵
}
Back(1);
cout << max_num << endl;
for (int i=1; i<=n; i++) //编号从1开始
{
cout << x[i] << " ";
}
return 0;
}旅行售货员问题
/*
7-1 旅行售货员
某售货员要到若干城市去推销商品,已知各城市之间的路程(或旅费)。他要选定一条从驻地出发,经过每个城市一遍,最后回到驻地的路线,使总的路程(或总旅费)最小。
输入格式:
第一行为城市数n
下面n行n列给出一个完全有向图,如 i 行 j 列表示第 i 个城市到第 j 个城市的距离。
输出格式:
一个数字,表示最短路程长度。
输入样例:
3
0 2 1
1 0 2
2 1 0
输出样例:
3
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 105;
int g[N][N];
int x[N];
int n;
int ans = 0x3f3f3f3f;
int now = 0;
void backtrack(int t) {//第t层表示已经到了第t - 1个城市
if (t > n) {//叶子节点,此时在第n个城市
if (now + g[x[n]][x[1]] < ans) {
ans = now + g[x[n]][x[1]];//回到驻点
}
} else {
for (int i = t; i <= n; i++) {
if (g[x[t - 1]][x[i]] != 0x3f3f3f3f && now + g[x[t - 1]][x[i]] < ans) {
swap(x[t], x[i]);
now += g[x[t - 1]][x[t]];
backtrack(t + 1);
now -= g[x[t - 1]][x[t]];
swap(x[t], x[i]);
}
}
}
}
int main() {
cin >> n;
memset(g, 0x3f, sizeof(g));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cin >> g[i][j];
}
}
for (int i = 1; i <= n; i++) x[i] = i;//初始化为1 2 3 4
backtrack(2);//从第二层开始遍历,第一层就是从驻地到其他城市
cout << ans;
return 0;
}
//不剪枝时间复杂度为O(n!)n 后问题
在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在n×n格的棋盘上放置n个皇后,任何个皇后不放在同一行或同一列或同一斜线上
输入格式:
一个数字n
输出格式:
按照深度优先输出所有可行的解
输入样例:
4
输出样例:
2 4 1 3
3 1 4 2解法一:
#include <iostream>
#include <cmath>
using namespace std;
const int MAX = 100;
int n;
int x[MAX];
bool fuc(int t) {
for(int i = 1; i < t; i++) {
if(x[t] == x[i] || abs(x[t] - x[i]) == abs(t - i)) {
return false;
}
}
return true;
}
void backtrack(int t) {
if(t > n) {
for(int i = 1; i <= n; i++) {
cout << x[i] << " ";
}
cout << endl;
}
for(int i = 1; i <= n; i++) {
x[t] = i;
if(fuc(t)) {
backtrack(t + 1);
}
}
}
int main() {
cin >> n;
backtrack(1);
return 0;
}
解法二:
/*
在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在n×n格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上
输入格式:
一个数字n
输出格式:
按照深度优先输出所有可行的解
输入样例:
4
输出样例:
2 4 1 3
3 1 4 2
*/
#include <iostream>
#include <cmath>
using namespace std;
const int MAX = 100;
int n;
int chosen[MAX] = { 0 };
int result[MAX];
bool check(int t) {
for (int i = 1; i < t; i++) {
if (abs(t - i) == abs(result[t] - result[i]) || result[t] == result[i]) {
return false;
}
}
return true;
}
void backtrack(int t) {
if (t > n) {
for (int i = 1; i <= n; i++) {
cout << result[i] << " ";
}
cout << endl;
}
for (int i = 1; i <= n; i++) {
if (chosen[i] == 0) {
chosen[i] = 1;
result[t] = i;
if (check(t)) {
backtrack(t + 1);
}
chosen[i] = 0;
}
}
}
int main() {
cin >> n;
backtrack(1);
return 0;
}最小机器重量问题
/*
7-2 最小重量机器设计问题
设某一机器由n个部件组成,每一种部件都可以从m个不同的供应商处购得。设wij是从供应商j 处购得的部件i的重量,cij是相应的价格。
试设计一个算法,给出总价格不超过d的最小重量机器设计。
输入格式:
第一行有3 个正整数n ,m和d, 0<n<30, 0<m<30, 接下来的2n 行,每行m个数。前n行是c,后n行是w。
输出格式:
输出计算出的最小重量,以及每个部件的供应商
输入样例:
3 3 4
1 2 3
3 2 1
2 2 2
1 2 3
3 2 1
2 2 2
输出样例:
在这里给出相应的输出。例如:
4
1 3 1
*/
#include<iostream>
using namespace std;
int n, m, cost; //限定价格 部件数 供应商数
int w[100][100];//w[i][j]为第i个零件在第j个供应商的重量
int c[100][100];//c[i][j]为第i个零件在第j个供应商的价格
int bestx[100];//bestx[i]用来存放第i个零件的最后选择供应商
int x[100];//x[i]临时存放第i个零件的供应商
int cw = 0, cc = 0, bestw = 100000;
void Backtrack(int t) // t对应 部件t
{
if (t > n)//搜索到叶子结点,一个搜索结束,所有零件已经找完
{
if (cw < bestw) {
bestw = cw; //当前最小重量
for (int j = 1; j <= n; j++)
bestx[j] = x[j];
}
// return; // 有else就不需要 return,两个选一个
}
else {
for (int i = 1; i <= m; i++) // 遍历所有供应商
{
cc += c[t][i];
cw += w[t][i];
x[t] = i;
if (cc <= cost && cw <= bestw) // 剪枝操作
Backtrack(t + 1);
cc -= c[t][i];
cw -= w[t][i];
}
}
}
int main()
{
cin >> n >> m >> cost;
for (int i = 1; i <= n; i++) //各部件在不同供应商的重量 cij:物品i在供应商j的价格
for (int j = 1; j <= m; j++)
cin >> c[i][j];
for (int i = 1; i <= n; i++) //各部件在不同供应商的价格 wij:物品i在供应商j的重量
for (int j = 1; j <= m; j++)
cin >> w[i][j];
Backtrack(1);
cout << bestw << endl; // 最低的重量
for (int i = 1; i <= n; i++) // 输出各个部件的供应商
cout << bestx[i] << " ";
return 0;
}
算法第六章、分支限界法(广度优先或者最小生成树)
分支限界法的基本思想:
不断的广度优先遍历所有的层次
从下一扩展结点的不同方式导致不同的分支限界法。
1、FIFO分支限界法
将活结点表组织成为一个队列,按先进先出原则选择下一个结点。
2、优先队列分支限界法
按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。
- 最大优先队列:使用最大堆,体现最大效益优先
- 最小优先队列:使用最小堆,体现最小费用优先广度优先搜索(BFS)和深度优先搜索(DFS)是图和树的两种基本遍历算法。它们的主要区别在于搜索节点的顺序和方式。
DFS 与 BFS 的区别
广度优先搜索(BFS)
广度优先搜索是一种分层遍历的算法,从起始节点开始,逐层扩展节点,直到找到目标节点或遍历完所有节点。BFS 通常使用队列(queue)来实现。
步骤:
- 将起始节点放入队列。
- 从队列中取出一个节点,访问它。
- 将该节点的所有未访问过的邻居节点放入队列。
- 重复步骤 2 和 3,直到队列为空。
特点:
- 逐层扩展:BFS 先访问离起始节点最近的节点,然后逐渐扩展到更远的节点。
- 最短路径:在无权图中,BFS 可以找到从起始节点到目标节点的最短路径。
- 空间复杂度高:由于需要存储所有节点的邻居,BFS 可能会占用较多的内存。
深度优先搜索(DFS)
深度优先搜索是一种沿着树或图的深度遍历的算法,尽可能深地搜索每个分支,直到无法继续,然后回溯到上一个节点,继续搜索其他分支。DFS 通常使用栈(stack)或递归来实现。
步骤(使用栈):
- 将起始节点放入栈。
- 从栈中取出一个节点,访问它。
- 将该节点的所有未访问过的邻居节点放入栈。
- 重复步骤 2 和 3,直到栈为空。
步骤(使用递归):
- 访问当前节点。
- 递归地访问当前节点的每个未访问过的邻居节点。
特点:
- 深度优先:DFS 会尽可能深地搜索每个分支,直到无法继续,然后回溯。
- 路径不一定最短:在无权图中,DFS 找到的路径不一定是最短路径。
- 空间复杂度低:由于 DFS 只需要存储当前路径上的节点,空间复杂度通常较低。
示例代码
BFS 示例(使用队列):
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
void bfs(vector<vector<int>>& graph, int start) {
queue<int> q;
vector<bool> visited(graph.size(), false);
q.push(start);
visited[start] = true;
while (!q.empty()) {
int node = q.front();
q.pop();
cout << node << " ";
for (int neighbor : graph[node]) {
if (!visited[neighbor]) {
q.push(neighbor);
visited[neighbor] = true;
}
}
}
}
int main() {
vector<vector<int>> graph = {
{1, 2},
{0, 3, 4},
{0, 5},
{1},
{1},
{2}
};
bfs(graph, 0);
return 0;
}DFS 示例(使用递归):
#include <iostream>
#include <vector>
using namespace std;
void dfs(vector<vector<int>>& graph, int node, vector<bool>& visited) {
visited[node] = true;
cout << node << " ";
for (int neighbor : graph[node]) {
if (!visited[neighbor]) {
dfs(graph, neighbor, visited);
}
}
}
int main() {
vector<vector<int>> graph = {
{1, 2},
{0, 3, 4},
{0, 5},
{1},
{1},
{2}
};
vector<bool> visited(graph.size(), false);
dfs(graph, 0, visited);
return 0;
}通过以上示例代码,可以直观地理解 BFS 和 DFS 的实现方式和区别。BFS 逐层扩展,适合寻找最短路径;DFS 深度优先,适合遍历所有路径。
例题
0-1 背包问题(FIFO)
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
struct Node {
int level; //该节点所在解空间树中的层次
int cw; //该节点的当前载重量
int cp; // 该节点的当前价值
};
queue <Node> q; // 定义队列
struct Obj {
double value;
double weight;
};//每件物品的重量及价值
Obj objs[101]; //定义存储n件物品的数组,方便调用sort函数
int bestv = 0;
int n, c;
double bound(int t,double cleft) {
double v = 0;
for(int i = t; i <= n; i++) {
if(objs[i].weight < cleft) {
v+=objs[i].value;
cleft=objs[i].weight;
} else {
v+= cleft*objs[i].value/objs[i].weight;
}
}
return v;
}
void bfs() {
Node node;
node.cp = 0;
node.cw = 0;
node.level = 1;
q.push(node);
while(!q.empty()) {
Node node = q.front();
q.pop();
if(node.level > n) {
if(node.cp > bestv){
bestv = node.cp;
}
continue;
}
if (node.cw + objs[node.level].weight <= c) {
//判断左分支是否入队
Node nextnode;
nextnode.level = node.level + 1;
nextnode.cw = node.cw + objs[node.level].weight;
nextnode.cp = node.cp + objs[node.level].value;
q.push( nextnode );
if ( bestv < nextnode.cp )
bestv = nextnode.cp;
//及时刷新暂时最优值,提高效率
}
if((node.cp + bound(node.level+1,c - node.cw)) > bestv) {
//判断右分支是否入队
Node nextnode;
nextnode.level = node.level + 1;
nextnode.cw = node.cw;
nextnode.cp = node.cp;
q.push(nextnode);
}
}
}
bool cmp(Obj a, Obj b){
return a.value/a.weight > b.value/b.weight;
}
int main() {
cin >> n>> c;
for(int i = 1; i <= n; i++) {
cin >> objs[i].weight >> objs[i].value;
}
sort(objs + 1, objs + 1 + n,cmp);
bfs();
cout << bestv << endl;
return 0;
}
0-1 背包(最小堆)
#include <iostream>
#include <queue>
#include <algorithm>
#include <cstdio>
using namespace std;
struct Node {
int level; //该节点所在解空间树中的层次
double cw; //该节点的当前载重量
double cv; // 该节点的当前价值
double uvalue; //该节点的上界 = 当前载重量 + 剩余容量的最大价值(采用背包问题的计算方法)
friend bool operator < (Node a, Node b) {
return a.uvalue < b.uvalue;
}
int x[110];
};
struct Obj {
double value;
double weight;
int preindex;
};//每件物品的重量及价值
const int MAXN = 110;
int n, c, bestc;
int bestx[MAXN];
Obj objs[MAXN];
priority_queue < Node > q; // 定义队列
bool cmp(Obj a, Obj b) { //用于sort排序时以单位重量价值降序排序
return a.value / a.weight > b.value / b.weight;
}
double bound(int t, double left)
//利用背包问题(贪心算法)计算剩余容量为left,可选物品为第t~n件时可装入的最大价值
{
double maxv = 0;
while ( t <= n && left >= objs[t].weight) {
maxv += objs[t].value;
left -= objs[t].weight;
t++;
}
if ( t <= n ) maxv += left * objs[t].value / objs[t].weight;
return maxv;
}
int bfs() {
//初始化根节点,加入队列
Node node;
node.level = 1;
node.cw = 0;
node.cv = 0;
node.uvalue = bound(1, c);
q.push(node);
while (!q.empty()) {
Node node = q.top(); //上界最大者出堆
q.pop();
//采用优先级队列,如果优先访问叶子节点,说明该叶子节点的上界值要高于其他所有待扩展节点的上界,
//由于该叶子节点的值与上界值相等,所以该叶子节点代表最优解,直接退出循环
if ( node.level > n ) {
bestc = node.cv;
for (int i = 0; i < n; i++)
bestx[i] = node.x[i];
break;
}
//约束函数,如果第level个物品可以装入背包,则左分支节点进入优先队列
if ( node.cw + objs[node.level].weight <= c ) {
Node nextnode;
nextnode.level = node.level + 1;
nextnode.cw = node.cw + objs[node.level].weight;
nextnode.cv = node.cv + objs[node.level].value;
nextnode.uvalue = node.uvalue;
//复制父节点到根的路径
for (int i = 1; i < node.level; i++)
nextnode.x[i] = node.x[i];
nextnode.x[node.level] = 1; //左孩子,路径为1
q.push(nextnode);//节点加入队列
}
//限界函数,如果右分支上界大于最优的中间结果,则进入优先队列
double uvalue = bound(node.level+1, c - node.cw) + node.cv;
if ( uvalue > bestc) {
Node nextnode;
nextnode.level = node.level + 1;
nextnode.cw = node.cw;
nextnode.cv = node.cv;
nextnode.uvalue = uvalue;
//复制父节点的到根的路径
for (int i = 1; i < node.level; i++)
nextnode.x[i] = node.x[i];
nextnode.x[node.level] = 0;//右孩子,路径为0
q.push(nextnode); //节点加入队列
}
}
return bestc;
}
int main() {
cin >> n >> c;
for (int i = 1; i <= n; i++) {
cin >> objs[i].weight >> objs[i].value;
objs[i].preindex = i;
}
//按单位重量价值一次性降序排序,便于后续贪心法计算上界
sort( objs + 1, objs + 1 + n, cmp );
//输出最优值
cout << "best value:" << bfs() << endl;
//输出最优解,所选物品的重量和价值
cout << "best plan:\nweight\tvalue" << endl;
for (int i = 1; i <= n; i++)
if (bestx[i] == 1)
cout << "选择了第" << objs[i].preindex << "个物品" << objs[i].weight << "\t" << objs[i].value << endl;
return 0;
}
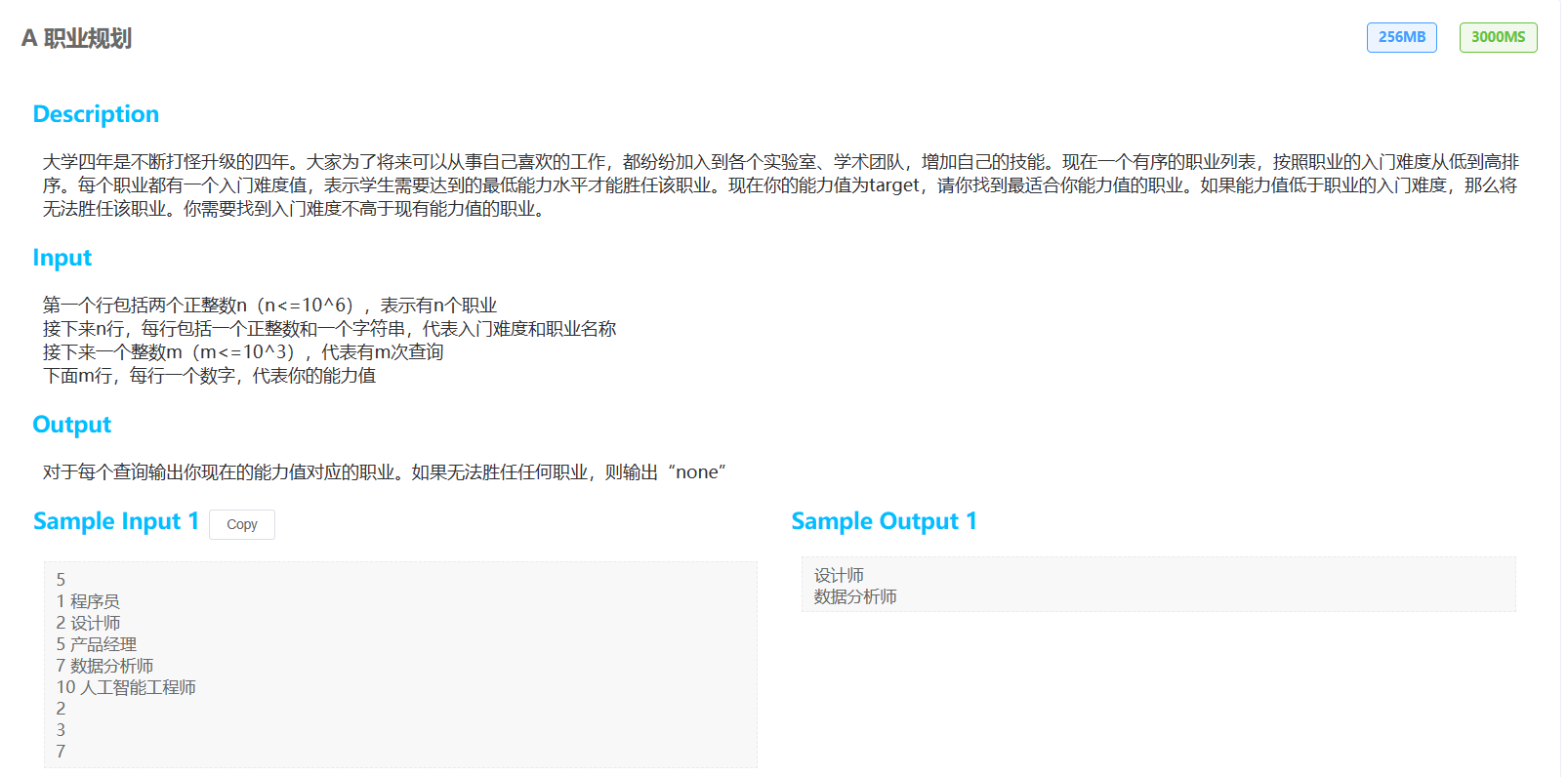
期中考试例题
#include <iostream>
#include <string>
using namespace std;
struct Course {
int difc;
string name;
};
int Search(Course courses[],int low, int top, int target) //a[n]是搜索数组,m为要搜索的元素,n是数组的长度
{
int i = 0;
int j = 0;
int middle = 0;
int detection = -1; //标志位
while (low <= top)
{
middle = (low + top)/2; //先计算该数组中间值下标
if (courses[middle].difc == target) //如果中间值等于要搜索的元素,则将标志位标记为中间值下标
detection=middle;
if (courses[middle].difc < target) //如果中间值小于要搜索的元素,即要查询元素在中间值右边,则将要查询数据左边界改成中间值之后一个的数据
{
low=middle+1;
}
else //如果中间值大于要搜索的元素,即要查询元素在中间值左边,则将要查询数据左边界改成中间值之前一个的数据
{
top=middle-1;
}
}
if (detection == -1) //如果m没有在其中,则执行完,top为底,low为顶,m在中间。
{
i = top;
j = low;
}
else
{
i = detection;
j = i;
}
//cout << "i的值为:" <<i<<endl<< "j的值为:"<<j<< endl;
return i;
}
int main() {
int n;
cin >> n;
Course courses[n];
for(int i = 0; i < n; i++) {
cin >> courses[i].difc >> courses[i].name;
}
int m;
cin >> m;
while(m > 0) {
int target;
cin >> target;
if(target < courses[0].difc){
cout << "none" <<endl;
m--;
continue;
}
int result = Search(courses, 0 , n-1, target);
cout << courses[result].name <<endl;
m--;
}
return 0;
}
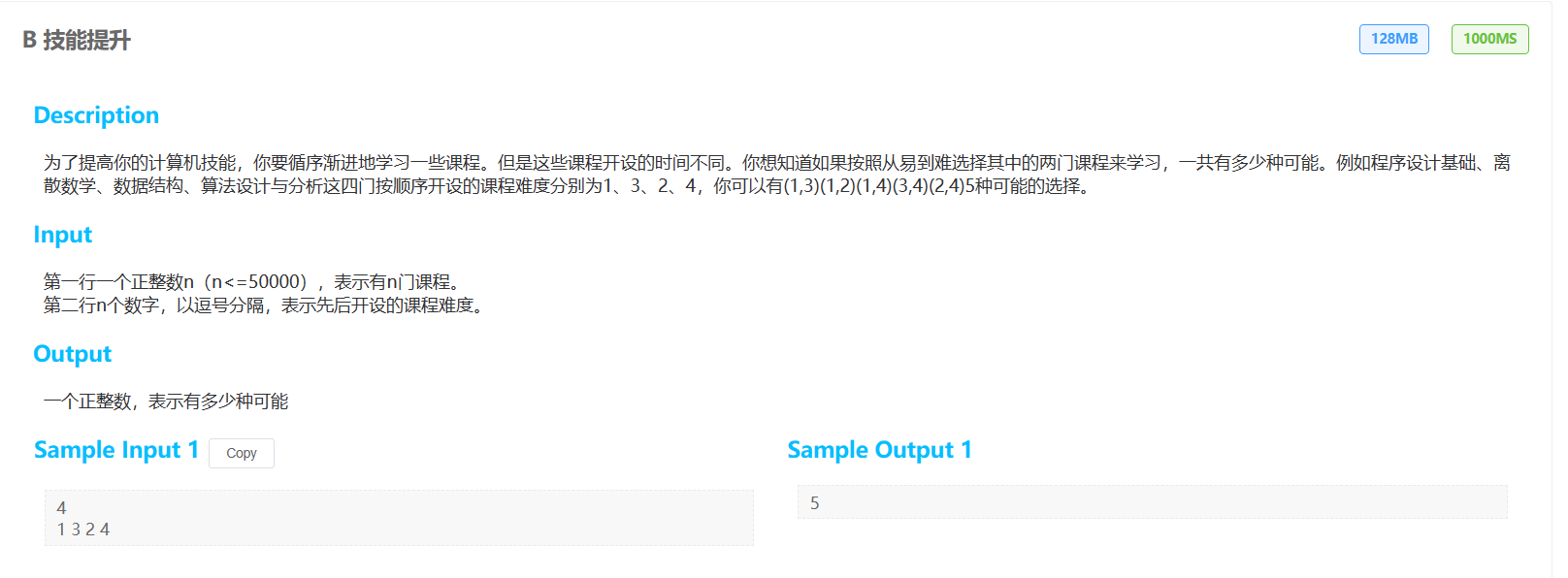
这是一个典型的逆序对或者顺序对问题有多种解法
#include <iostream>
using namespace std;
#define MAX 5000
int nums[MAX];
int total;
int sum;
void merge(int arr[], int temp[], int left, int mid, int right);
void mergeSort(int arr[], int left, int right) {
if (left >= right) {
return;
}
int mid = left + (right - left) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
int temp[right - left + 1];
merge(arr, temp, left, mid, right);
}
void merge(int arr[], int temp[], int left, int mid, int right) {
int i = left;
int j = mid + 1;
int index = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {//解法1:改成>=原来的逆序对数目变顺序对
sum += right - j +1;
temp[index] = arr[i];
index++;
i++;
} else {
total += mid - i + 1;// 统计逆序对的数量
temp[index] = arr[j];
index++;
j++;
}
}
while (i <= mid) {
temp[index] = arr[i];
index++;
i++;
}
while (j <= right) {
temp[index] = arr[j];
index++;
j++;
}
for (int k = 0; k < index; k++) { // 把临时数组复制回原数组
arr[left + k] = temp[k];
}
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> nums[i];
//解法2: nums[i] = - nums[i];
}
mergeSort(nums, 0, n-1);
cout << "逆序对的数量:" << total << endl;
cout << "顺序对的数量: " << sum << endl;
return 0;
}最长公共子序列问题
#include <iostream>
#include <string>
using namespace std;
#define MAX 1000
string course[MAX];
string myc[MAX];
int dp[MAX][MAX];
// 输出选择的课程名字
void printLCS(int i, int j) {
// 递归终止条件
if (i == -1 || j == -1) {//因为下标选择从1开始
return;
}
// 如果当前课程相同,表示选择了这门课程
if (course[i] == myc[j]) {
printLCS(i-1, j-1);
cout << course[i] << " ";
}
// 如果dp[i-1][j]大于dp[i][j-1],表示选择了当前课程的前一个课程
else if (dp[i-1][j] > dp[i][j-1]) {
printLCS(i-1, j);
}
// 如果dp[i-1][j]小于dp[i][j-1],表示选择了当前课程的后一个课程
else if (dp[i-1][j] < dp[i][j-1]) {
printLCS(i, j-1);
}
// 如果dp[i-1][j]等于dp[i][j-1],表示有多种选择,优先选择开课时间靠前的方案,选择了当前课程的前一个课程
else {//因为要选开课方案前的,所以优先淘汰开课时间后的方案
printLCS(i-1, j);
}
}
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < n; i++) {
cin >> course[i];
}
for (int i = 0; i < m; i++) {
cin >> myc[i];
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (course[i-1] == myc[j-1]) {
dp[i][j] = dp[i-1][j-1] + 1;
}
else if (dp[i-1][j] > dp[i][j-1]) {
dp[i][j] = dp[i-1][j];
}
else {
dp[i][j] = dp[i][j-1];
}
}
}
// 输出选择的课程数量
cout << dp[n][m] << endl;
// 输出选择的课程名称
printLCS(n, m);
return 0;
}
双指针
【Leetcode】接雨水(双指针、单调栈)_接雨水双指针-CSDN博客
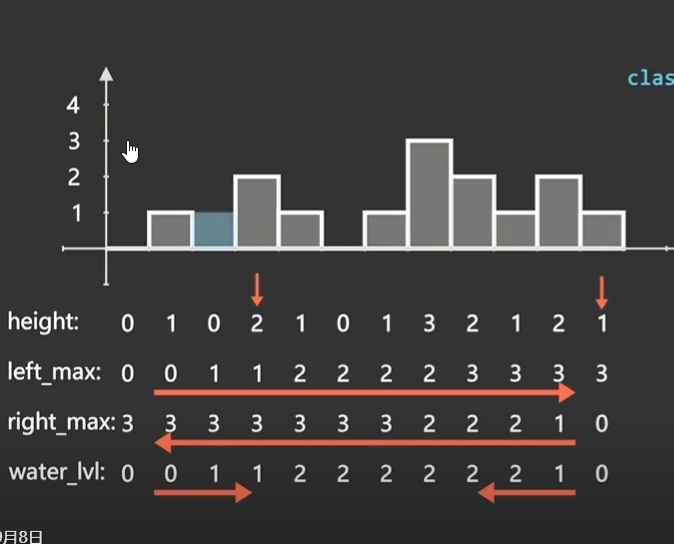
1. 接雨水问题
解法一:普通解法
假设每个宽度为1的柱子那里有一个高度未知的宽度为1的水桶,这个水桶能接的水就是当前柱子所处位置能留下的雨水,而水桶的左边木板的高度取决于当前柱子左边所有的柱子中最高的那个柱子的高度,水桶右边木板的高度取决于当前柱子右边所有的柱子中最高的柱子的高度,而水桶左右木板中较小的那个木板的高度减去当前柱子的高度就是当前水桶能接到的水,也就是当前位置留下的雨水。
int getRain_1(const vector<int> &heights, vector<int> &left_max, vector<int> &right_max)
{
int rainCount = 0;
left_max[0] = 0;
right_max[heights.size() - 1] = 0; // 最右边的
for (int i = 1; i < heights.size(); i++)
{
left_max[i] = max(left_max[i - 1], heights[i - 1]);
right_max[heights.size() - i - 1] = max(heights[heights.size() - i], right_max[heights.size() - i]);
}
for (int j = 0; j < heights.size(); j++)
{
rainCount += max(0, min(left_max[j], right_max[j]) - heights[j]);
}
return rainCount;
}解法二:双指针
由第一种解法的left_max数组和right_max数组可以得出递增/递减的关系,
因为短板效应,对应位置的水位只和左边或者右边的较小最高值有关,因此我可以使用双指针,分别指向数组首和尾,
在遍历过程中动态的记录最高值,确保当前位置的水位是较小最高值就可以
刚好是left_max和right_max数组最小的开始,假如left_max小于right_max(说明当前位置的左边最高都不超过右边的非最高值),那么left指针指向的水位就等于left_max,(接雨水总量 += left_max - 当前柱子高度),然后左指针向右移一位,右边同理
int getRain_2(const vector<int> &heights) // 双指针
{
// left_max数组是从左到右递增,因为越往右越有可能遇到更高的
// right_max数组是从右到左递增,因为越往左遍历遍历的柱子越多,越有可能遇到更高的
// 当前位置的水位是山峰型,中间高,两边低,因为越往中间两边的柱子越多,越可能出现高柱子截住水流的情况
int left = 0;
int right = heights.size() - 1;
int left_max = 0;
int right_max = 0; // 左右指针移动中遍历到的最大值
int rainCount = 0;
while (left <= right) // 此处需要是 <= 否则会出现左右指针交会的那根柱子没计算雨水累计
{
if (left_max <= right_max)
{
rainCount += (left_max - heights[left]) >= 0 ? left_max - heights[left] : 0; // 注意处理当前柱子很高的情况,不要加上负数了
left_max = max(left_max, heights[left]); // 更新最大值
left++;
continue;
}
else
{
rainCount += (right_max - heights[right]) >= 0 ? right_max - heights[right] : 0;
right_max = max(right_max, heights[right]);
right--;
continue;
}
}
return rainCount;
}滑动窗口
滑动窗口算法通常用于处理数组或字符串中的连续子数组或子字符串问题,它可以将嵌套的循环问题,转换为单循环问题,降低时间复杂度。
1. k长度最大子段和
给定一个整数数组,计算长度为 ‘k’ 的连续子数组的最大总和。
首先很容易想到使用暴力破解,每个位置都遍历一次,求最大值
// 暴力破解
int test01(const vector<int> nums, int k) // k表示子段长度
{
int sum = INT_MIN;
for (int i = 0; i < nums.size() - k + 1; i++) // 此处省略掉短于k的子段
{
int new_sum = 0;
for (int j = i; j < i + k; j++)
{
new_sum += nums[j];
}
sum = max(sum, new_sum);
}
return sum;
}滑动窗口
但是滑动窗口非常适合用来处理子串的问题,例如同一个问题,我们假定一个长度为k的窗口,不断移动窗口的位置,只用将窗口从左往右移动一轮,就能得出在过程中不断变化的maxSum
// 滑动窗口
int test02(const vector<int> nums, int k)
{
int current_sum = 0;
// 初始化第一个窗口大小
for (int i = 0; i < k; i++)
{
current_sum += nums[i];
}
int maxSum = current_sum;
// 滑动窗口,每次滑动移动一个单位,同时当前窗口和 `减去左边移出的` `加上右移入的`
for (int i = 1; i < nums.size() - k + 1; i++)
{
current_sum = current_sum - nums[i - 1] + nums[i + k - 1];
maxSum = max(current_sum, maxSum);
}
return maxSum;
}2. 最小包含子串
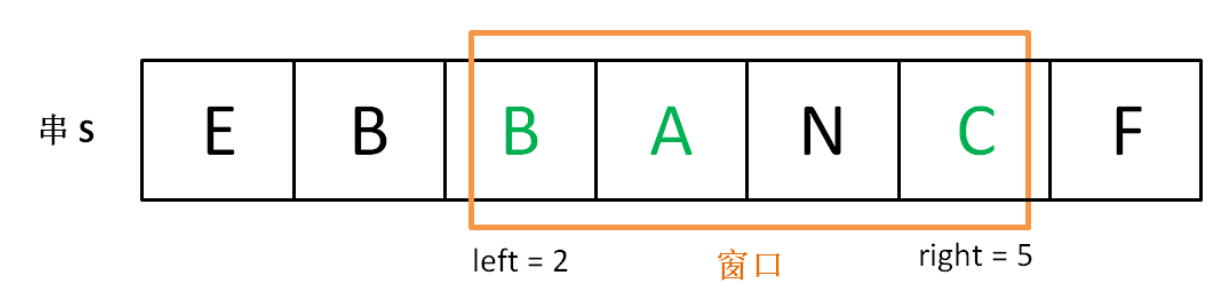
题目要求:给定一个字符串 S 和一个字符串 T,请在 S 中找出包含 T 所有字母的最小子串。(minimum-window-substring)
示例输入输出:
假设一个窗口已处于父串中,有两种情况:
- 没找到全部字母 -> 向右侧扩大窗口,直到找到全部字母
- 找到全部字母 -> 是否是最小? 从左边缩小窗口,直到无法继续缩小后记录,
继续向右遍历(右侧可能存在没被遍历的更小子串)
#include <iostream>
#include <vector>
#include <unordered_map>
#include <climits> // 用于INT_MAX
using namespace std;
string test01(const string str, const string substr)
{
int left = 0; // 窗口左边界
int right = 0; // 右边界初始化为0
int min = INT_MAX; // 记录当前找到匹配的子串的长度,初始化为最大值
string result = ""; // 最终结果
// charCount用来记录窗口应该出现的字符和次数
// 为正数表示还应该出现n次
// 为负数表示不应该出现,但是此时窗口中包含
unordered_map<char, int> charCount;
for (char c : substr)
{
charCount[c]++; // 自动处理不存在的情况(初始化为0后+1)
}
// 等待匹配的字符数量,初始值为子串的长度
int wait_for_pattern = substr.size();
vector<string> results; // 用于存储所有可能的结果
while (right < str.size()) // 边界处理,滑动窗口不会超出
{
// 如果当前字符在子串中存在
if (charCount[str[right]] > 0)
{
wait_for_pattern--; // 减少一个要匹配的字符数
}
// 无论当前字符是否在子串中,都将其计数减1,表示纳入窗口内
charCount[str[right]]--;
right++; // 右指针向右移动
// 当所有字符都匹配时
while (wait_for_pattern == 0)
{
// 如果当前窗口长度小于之前记录的最小长度
if (right - left < min)
{
min = right - left; // 更新最小长度
// 更新结果字符串,substr参数为起始位置和长度
result = str.substr(left, min);
}
// 尝试左缩窗口,即移动左指针
// 将左指针指向的字符的计数加1
charCount[str[left]]++;
// 如果该字符在子串中存在且计数大于0,说明需要重新匹配这个字符
if (charCount[str[left]] > 0)
{
wait_for_pattern++;
}
left++; // 左指针向右移动
}
}
// 如果min仍为INT_MAX,说明没有找到符合条件的子串,返回空字符串
return min == INT_MAX ? "" : result;
}
int main(int argc, char const *argv[])
{
string fullStr = "ADOBECODEBANC";
string targetSubStr = "ABC";
string minSubStr = test01(fullStr, targetSubStr);
cout << minSubStr << endl;
return 0;
}