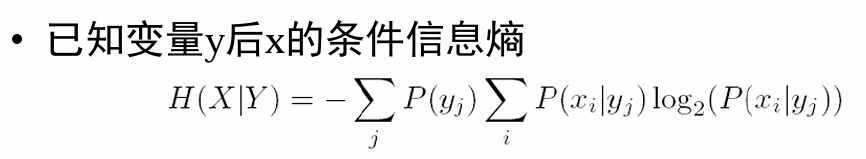课程资源
【决策树】深入浅出讲解决策树算法(原理、构建)_决策树算法原理-CSDN 博客
决策树 C4.5 算法的技术深度剖析、实战解读 - techlead_krischang - 博客园 (cnblogs.com)
1.绪论
1.1 数据挖掘的重要性
- 背景: 数据爆炸但知识贫乏
人们积累的数据越来越多。但是,目前这些数据还仅仅应用在数据的录入查询、统计等功能,无法发现数据中存在的关系和规则,无法根据现有的数据预测未来的发展趋势,导致了**”数据爆炸但知识贫乏”**的现象。
- 从商业数据到商业智能的进化
| 进化阶段 | 商业问题 | 支持技术 | 产品特点 |
|---|---|---|---|
| 数据搜集 (60 年代) | “过去五年中我的总收入是多少?” | 计算机、磁带和磁盘 | 提供历史性的、静态的数据信息 |
| 数据访问 (80 年代) | “在新英格兰的分部去年三月的销售额是多少?” | 关系数据库(RDBMS)结构化查询语言(SQL)ODBC | 在记录级提供历史性的、动态的数据信息 |
| 数据仓库决策支持 (90 年代) | “在新英格兰的分部去年三月的销售额是多少?波士顿据此可得出什么结论?” | 联机分析处理(OLAP)多维数据库数据仓库 | 在各种层次上提供动态的数据信息 |
| 数据挖掘 (正在流行) | “下个月波士顿的销售会怎么样?为什么?” | 高级算法多处理器计算机海量数据库 | 提供预测性信息 |
- 科学发展范式
| 分类 | 时间段 | 发展内容 |
|---|---|---|
| 经验科学 | Before-1600 | 两个铁球同时落地 |
| 理论科学 | 1600-1950s | 集合论、图论、数论和概率论 |
| 计算科学 | 1950s-1990s | 人工智能 1.0(简单的优化、贪婪算法) |
| 数据科学 | 1990-now | 数据挖掘、人工智能 2.0(以数据为基础的强化学习) |
1.2 数据挖掘的定义和概念
- 数据挖掘是从大量的、不完全的、有噪声的、模糊的随机的数据中提取隐含在其中的、人们事先不知道的但又是潜在有用的信息和知识的过程。
- Data Mining is the process of automatically extracting interesting and useful hidden patterns from usually massive, incomplete and noisy data.[Wikipedia]
引入
聊聊经典案例”啤酒与尿布”的本质:关联分析 - 知乎 (zhihu.com)
数据分析里有一个经典的案例,沃尔玛超市里经常会把婴儿的尿不湿和啤酒放在一起售卖,原因是经过数据分析发现,出来买尿不湿的家长以父亲居多,如果他们在买尿不湿的同时看到了啤酒,将有很大的概率购买,这样就可以提高啤酒的销售量。
数据、信息、知识

- “8,000”和”10,000”是数据。
- “8,000 米是飞机飞行最大高度”与”10,000 米的高山”是信息。
- “飞机无法飞越这座高山”是知识。
- “飞机必须飞得比山高”是智慧。
1.3 数据挖掘的主要内容
关联规则挖掘

根据购买的数据,分析的出,购买牛奶的顾客,更可能同时买了面包,这两样东西具有关联性
于是,在超市中,经常会看到用胶布把牛奶和面包(或者其他)进行捆绑销售,防止因为需要跑来跑去减少销量(增加顾客工作量),这就是关联性
分类
分类是指将数据集中的对象或实例分配到预先定义的类别或标签中。它是一种监督学习的方法

分类分析步骤
- 学习建模, 通过大量的训练集学习建立模型
- 分类测试, 将大量的新数据通过数据模型进行测试,查看输出结果是否符合预期
聚类
不先训练模型,在通过模型预测,通常使用相似性算法,不断地进行算法,最后得出输出

分类和聚类的区别
- 非监督式学习
- 比如有一群白色和黑色的玩偶,你天然的知道要将白色的放到一起,黑色的放到一堆
- 监督式学习
- 你在一个广场上站着,不断的有男性来问你男厕所在哪,女性来问女厕所在哪,所以,你归纳出,男生就要去男厕所,在这之后,再有人来问,你会根据你的经验提前预知到他将要问什么
回归

1.4 数据挖掘的过程

数据清洗
为什么要进行数据清洗?
现实世界的数据是”脏的”
不完整的:有感兴趣的属性缺少属性值,可以采取(忽略属性列,自动填充缺失值)
含噪声的:包含错误的或是”孤立点” (平滑噪声)
不一致的:在命名或是编码上存在差异 (数据变换 -> 规范化 / 离散化即
概念分层利用分类值标记替换连续属性的数值)最小 - 最大规范化
对于将数据缩放到 [0, 1] 范围内的公式:$$ x’ = \frac{x - x_{\text{min}}}{x_{\text{max}} - x_{\text{min}}} $$
对于将数据缩放到任意范围 [a, b] 的公式:$$ x’ = a + \frac{(x - x_{\text{min}})(b - a)}{x_{\text{max}} - x_{\text{min}}} $$
意义
数据清理的目的就是试图填充缺失值、去除噪声并识别离群点、纠正数据中的不一致值
习题
- 人从出生到长大的过程中,是如何认识事物的?(B)
A. 先分类,后聚类
B. 先聚类,后分类 - 离群点一定是负面的吗?(不一定)
答: 离群点(Outliers)在数据分析和统计学中通常指的是那些与大多数数据点显著不同的数据点,它们可能包含以下几种情况:
数据错误:离群点可能是由于数据收集或录入错误导致的,这种情况下它们确实是”坏”的,因为它们不代表真实的数据情况。
异常事件:在某些情况下,离群点可能代表一些异常但真实发生的事件。例如,在销售数据中,某个产品在某一天的异常高销量可能是由于特殊促销活动导致的。
新趋势或模式的指示:离群点有时可以指示新的趋势或模式。例如,在股票市场中,某些异常的价格波动可能是新趋势开始的信号。
数据多样性:在某些研究中,离群点可能代表数据集的多样性,反映了不同群体或条件的存在。
2.认识数据和统计
2.1 数据类型和统计
数据对象
- 数据集由数据对象组成
- 一个数据对象代表一个实体(每行代表一个数据对象)
- 称为样品,示例,实例,数据点,对象,元组(tuple)
- 数据对象所描述的属性
- 数据库中的行 -> 数据对象
- 列 -> “属性”
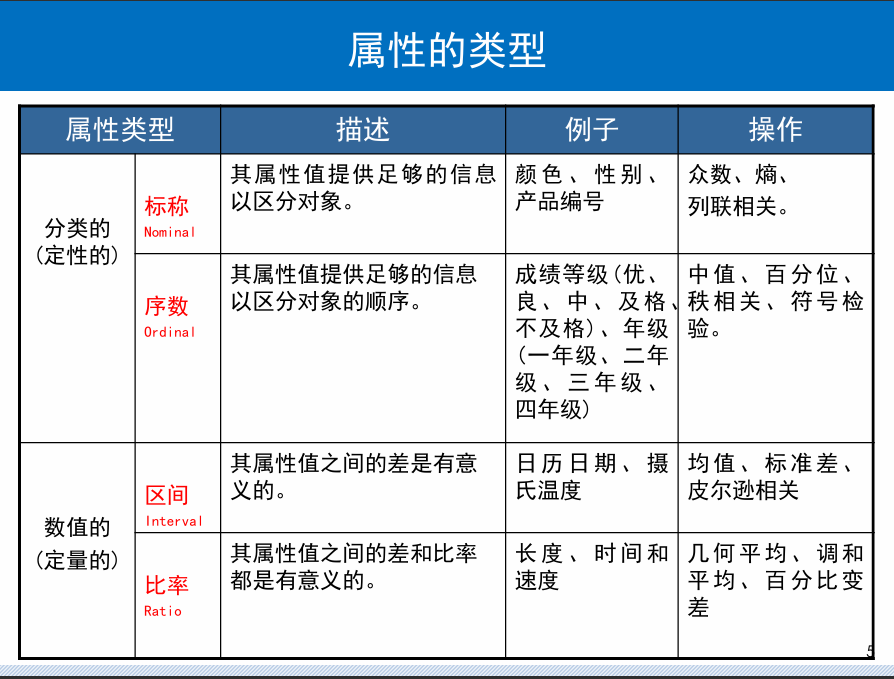
属性的类型
常见的四类属性:
标称(Nominal): 状态,类别可列举
- Examples: ID numbers, zip codes
- Hair color={黑色,棕色,灰色,白色} 婚姻状况{已婚,未婚},职业,身份证号码,邮政编码
- 二进制类型数据: 只有 2 个状态(0 和 1)的属性,对称二进制两种(例如,性别) 不对称的二进制例如,(医疗测试的正面与负面)所谓对称,是指两种状态的数据规模是否大致相当
序数(Ordinal)
- Examples: rankings (e.g., taste of potato chips on a scale from 1-10),grades, height in {tall, medium, short})
- 有一个有意义的顺序(排名),但不知道连续值之间的大小。大小={小,中,大},等级,军队排名
区间标度(Interval)
- Examples: calendar dates,temperatures in Celsius or Fahrenheit.
- 以单位长度顺序性度量
- 值有序,比如温度、日历等
- 不存在 0 点,倍数没有意义:我们平常通常不说 2000 年是 1000 年的 2 倍。
比率(Ratio)
- Examples: temperature in Kelvin, length, time, counts
- 具有固定零点的数值属性,有序且可以计算倍数,长度、重量等
有关属性的问题
常见的四类属性:
- 标称(Nominal): 标称属性的数据分类模型有哪些?
- 序数(Ordinal): 序数类型的数据求均值是否合理?能否用
k-means算法 - 区间(Interval): 区间标度属性特征工程时,是否可以采用乘法原则?
- 比率(Ratio): 哪些数据挖掘算法适用于比率标度属性?
数据集的类型
记录数据
事务数据(Transaction Data): 是一种特殊类型的记录数 据,其中每个记录涉及一个项的集合。常见的事务数据如超市零售数据,客户一次购物所购买的商品集合就构成一个事务,而购买的商品就是项。这种 类型的数据也称作购物篮数据(Market Basket Data)数据矩阵: 如果一个数据集中的所有数据对象都具有相同的数值属性集,则数据对象可以看作多维空间中的点,其中每个维代表描述对象的一个不同属性,数据集可以用一个m×n的矩阵表示,其中m行,一个对象一行;n列,一个属性一列文本数据: 文档用词向量表示- 每一个词都是向量的一个分量(属性)
- 每个分量的值是对应词在文档中出现的次数
| 文档 / 词 | team | coach |
|---|---|---|
| document1 | 0 | 2 |
| document2 | 4 | 1 |
| document3 | 2 | 3 |
图形数据
如 化合物结构

有序数据
时序数据
序列数据,如DNA序列
数据统计汇总
- 动机
- 为了更好地理解数据:中性化趋势,分布趋势
- 数据的统计特性
- 最大值,最小值,中位数,位数,离群值,方差等。
中性化趋势度量:均值、中位数和众数

- 平均值一组数据的均衡点。但是,均值对离群值很敏感。
- 因此,中位数和截断均值也很常用。
- 众数指一组数据中出现次数最多的数据值。

- 箱线图(boxplot):
min, Q1, median, Q3, max;单独添加胡须表示离群点。 截断均值: (p=40%),对于数据去除百分之40的数据点(分别从高端和低端丢弃20%),然后按常规方法取均值

2.2 数据可视化
数据可视化分析之箱线图分析
箱线图(Boxplot),也称为盒须图、盒式图或箱型图,是一种用于显示一组数据分布情况的统计图。它通过五个关键数值来描述数据的分布特征:最小值(min)、第一四分位数(Q1)、中位数(median)、第三四分位数(Q3)和最大值(max)。箱线图能够直观地展示数据的中心位置、分散程度以及是否存在异常值。
箱线图的组成部分
- 箱体(Box):箱体的上下边界分别对应第一四分位数(Q1)(25%的数据小于或等于 Q1,75%的数据大于 Q1)和第三四分位数(Q3),箱体的长度(Q3 - Q1)称为四分位距(IQR),表示数据的中间 50%的分布范围。
- 中位数(Median):箱体中间的线表示数据的中位数,即第二四分位数(Q2),它反映了数据的中心位置。
- 胡须(Whiskers):箱体外的两条线称为胡须,通常表示数据的最大值和最小值。但在实际应用中,胡须的长度通常有限制,一般不超过 1.5 倍的四分位距(1.5 * IQR)。超过这个范围的点被认为是离群点(Outliers)。
- 离群点(Outliers):在胡须之外的点被认为是离群点,通常用单独的点或符号表示,这些点可能是数据中的异常值。
箱线图的优点
- 直观展示数据分布:箱线图能够直观地展示数据的分布情况,包括中心位置、分散程度和异常值。
- 比较不同组数据:通过并排显示多个箱线图,可以方便地比较不同组数据的分布特征。
- 识别异常值:箱线图能够帮助识别数据中的异常值,这些异常值可能是数据录入错误或真实存在的极端值。
箱线图的应用场景
- 数据探索:在数据分析初期,使用箱线图可以帮助快速了解数据的分布特征。
- 质量控制:在生产过程中,箱线图可以用于监控产品质量,及时发现异常。
- 统计分析:在统计学中,箱线图常用于描述性统计分析,展示数据的分布情况。

箱线图能够分析多个属性数据的分布差异性
- 鸢尾花的案例
https://blog.csdn.net/H_lukong/article/details/90139700
https://www.cnblogs.com/star-zhao/p/9847082.html
- 一个数据集有四个属性
- 花萼宽度
- 花萼长度
- 花瓣宽度
- 花瓣长度
- 三种类别 lris Setosa , lris Versicolour , lris Virginica
数据可视化之直方图
- 用来分析单个属性在各个区间变化分布
- 直方图可视化发现特征对类别的区别性
通过不同类别的各个属性的直方图,例如lris Setosa的花萼宽度近似于μ = 3的正态分布,而lris Versicolour近似于μ = 2,lris Virginica近似于μ = 1,就可以得出花萼宽度可以区分类别的简单结论
数据可视化之散点图
用来显示两组数据的相关性分布
用来显示两组数据的类别分布(男性和女性身高体重的散点图,靠近坐标原点的可能性更接近于女性)

分为正相关、负相关、不相关(不线性相关)
- 房价预测案例

房屋面积(1)和建筑面积(3)相关性更强
2.3 数据相似性
简单数据对象 x 和 y 的相似度或相异度
| 数据类型 | x 与 y 的相似度 | 相异度 |
|---|---|---|
| 标称 | s = 1 (if x = y) s = 0 (if x != y) |
d = -s |
| 序数 | s = 1 - d | d = |x - y| / (n - 1) n 为值的个数,值映射到 0 ~ n-1 |
| 区间/比率 | s = -d, s = 1 / (1 + d)…等单调递减函数 | d = |x - y| |
度量数据的相似性和相异性

- 相似度 Similarity
- 度量两个数据对象有多相似
- 值越大就表示数据对象越相似
- 通常取值范围为[0,1]
- 相异度 Dissimilarity(e.g. distance)
- 度量两个数据对象的差别程度
- 值越小就表示数据越相似
- 最小相异度通常为 0
- 邻近性 Proximity
- 指相似度或者相异度
标称属性的邻近性度量
- 标称属性可以取两个或多个状态
- 方法: 简单匹配
| id | 属性 1 | 属性 2 | 属性 3 | 属性 4 |
|---|---|---|---|---|
| 1 | 弹琴 | 跳高 | 唱歌 | 背诗 |
| 2 | 弹琴 | 跳远 | 跳舞 | 读书 |
$$ d(i,j) = \frac{p - m}{p} $$ $$d(1,2) = \frac{4 - 1}{4} $$
m:匹配次数,p: 属性总数
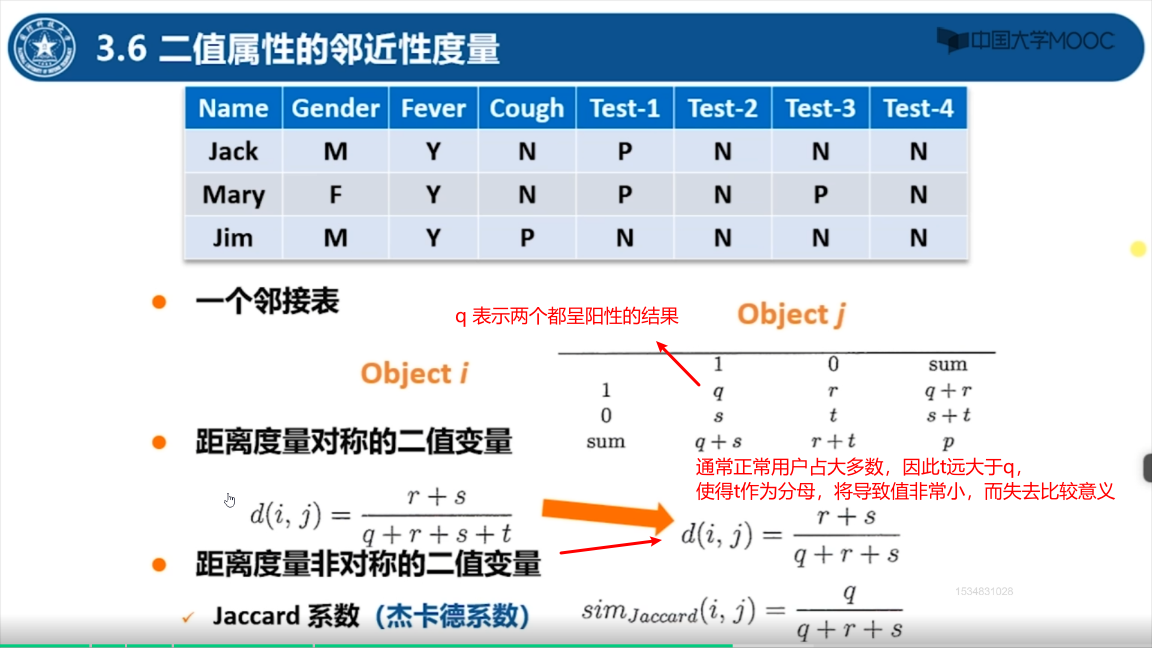
二值属性的邻近性度量例子
- Gender 是对称属性,其余都是非对称属性,假设只计算非对称属性
- Y 和 P 的值为 1(阳性),N 的值为 0(阴性正常)
- test1-4 表示抽血化验的结果
- SMC(简单匹配系数) = ( M_11 + M_00 ) / ( M_11 + M_00 + M_10 + M_01)
数值属性的邻近性度量
| point | attribute 1 | attribute 2 |
|---|---|---|
| x1 | 1 | 2 |
| x2 | 3 | 5 |
| x3 | 2 | 0 |
| x4 | 4 | 5 |
$$ d(i,j) = \left( |x{i1} - x{j1}|^h + |x*{i2} - x*{j2}|^h + \ldots + |x*{ip} - x*{jp}|^h \right)^{\frac{1}{h}} $$**
- 性质
- d(i,j) > 0 if i≠j,and d(i,i)=0**(正定性)**
- d(i,j) = d(j, i)(对称性)
- d(i, i) ≤ d(i, k) + d(k,i)(三角不等性)

2.4 数据对象之间的相异度
例题
计算向量$$\mathbf{A} = (1, 1, 0, 0)$$ 和$$\mathbf{B} = (0, 1, 1, 0)$$ 的余弦相似度和欧几里得距离。
1. 余弦相似度
余弦相似度是通过测量两个向量的夹角的余弦值来确定它们之间的相似性。公式为:
$$\text{余弦相似度} = \cos(\theta) = \frac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{A}| |\mathbf{B}|}$$
计算步骤:
计算点积$$\mathbf{A} \cdot \mathbf{B} $$:
$$ \mathbf{A} \cdot \mathbf{B} = 1 \cdot 0 + 1 \cdot 1 + 0 \cdot 1 + 0 \cdot 0 = 0 + 1 + 0 + 0 = 1 $$计算向量$$\mathbf{A}$$ 的模 $$|\mathbf{A}|$$ :
$$|\mathbf{A}| = \sqrt{1^2 + 1^2 + 0^2 + 0^2} = \sqrt{1 + 1 + 0 + 0} = \sqrt{2} $$计算向量$$\mathbf{B}$$ 的模$$|\mathbf{B}|$$ :
$$||\mathbf{B}| = \sqrt{0^2 + 1^2 + 1^2 + 0^2} = \sqrt{0 + 1 + 1 + 0} = \sqrt{2}$$计算余弦相似度:
$$\cos(\theta) = \frac{1}{\sqrt{2} \cdot \sqrt{2}} = \frac{1}{2} = 0.5 $$
2. 欧几里得距离
欧几里得距离是两个点在欧几里得空间中的直线距离。公式为:
$$\text{欧几里得距离} = |\mathbf{A} - \mathbf{B}| = \sqrt{\sum_{i=1}^{n} (A_i - B_i)^2}$$
计算步骤:
计算向量差$$\mathbf{A} - \mathbf{B}$$ :
$$\mathbf{A} - \mathbf{B} = (1 - 0, 1 - 1, 0 - 1, 0 - 0) = (1, 0, -1, 0)$$计算差的平方:
$$(1 - 0)^2 + (1 - 1)^2 + (0 - 1)^2 + (0 - 0)^2 = 1^2 + 0^2 + (-1)^2 + 0^2 = 1 + 0 + 1 + 0 = 2$$计算欧几里得距离:
$$||\mathbf{A} - \mathbf{B}| = \sqrt{2}$$
最终答案
- 余弦相似度:$${0.5}$$
- 欧几里得距离:$${\sqrt{2}}$$
2.5 数据相关性
线性相关系数
线性相关系数,通常指的是皮尔逊相关系数(Pearson correlation coefficient),用于度量两个变量之间的线性相关程度。其计算公式如下:
$$ r = \frac{\sum*{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum*{i=1}^{n} (Xi - \bar{X})^2} \sqrt{\sum{i=1}^{n} (Y_i - \bar{Y})^2}} $$
相关系数 ( r ) 的取值范围在 -1 到 1 之间:
- ( r = 1 ) 表示完全正相关。(平行向量)
- ( r = -1 ) 表示完全负相关。(反向向量)
- ( r = 0 ) 表示没有线性相关。
离散属性对象之间的相关性
- 对称的不确定性
- 离散数据之间相关性(互信息)
- 熵,特征 x 的信息熵(度量信息量的大小)
熵是信息论中的一个重要概念,用于度量信息的不确定性。熵的公式如下:
对于离散随机变量 ( X ) ,其可能的取值为 ( $$x_1, x_2$$,$$\ldots, x_n $$) ,对应的概率为 ($$ P(X = x_i) = p_i $$) , (其中 ($$ i = 1, 2, \ldots, n $$)),则熵 ( H(X) ) 定义为:

其中:
- ( H(X) ) 表示随机变量 ( X ) 的熵。
- ( p_xi ) 是随机变量 ( X ) 取第 ( i ) 个值的概率。
- ( log_2 ) 是以 2 为底的对数。
熵的单位是比特(bit),表示为了准确描述随机变量 ( X ) 的值,平均需要的二进制位数。
对于连续随机变量,熵的计算需要用到概率密度函数 ( f(x) ) ,熵的表达式为:
$$H(X) = -\int_{-\infty}^{+\infty} f(x) \log_2 f(x) dx$$
这里 ( f(x) ) 是随机变量 ( X ) 的概率密度函数,积分是在 ( X ) 的整个取值范围上进行的。
熵越小表示样本对目标属性的分布越纯,反之熵越大表示样 本对目标属性分布越混乱
条件熵
条件熵 ( H(X|Y) ) 表示在已知随机变量 ( Y ) 的情况下随机变量 ( X ) 的不确定性。条件熵的公式如下:
$$H(X|Y) = \sum_{i=1}^{n} \sum_{j=1}^{m} p(x_i, y_j) \log_2 \frac{p(x_i, y_j)}{p(y_j)}$$
其中:
- ( H(X|Y) ) 表示给定 ( Y ) 的条件下 ( X ) 的条件熵。
- ( p(x_i, y_j) ) 是联合概率分布,即 ( X ) 取第 ( i ) 个值同时 ( Y ) 取第 ( j ) 个值的概率。
- ( p(y_j) ) 是边缘概率分布,即 ( Y ) 取第 ( j ) 个值的概率。
条件熵 ( H(X|Y) ) 可以解释为在已知 ( Y ) 的情况下,为了确定 ( X ) 还需要多少信息。
2.6 信息增益
信息增益是决策树算法中一个重要的概念,特别是在 ID3、C4.5 等算法中用来选择特征。信息增益表示得知特征 ( Y ) 的信息而使得类 ( X ) 的不确定性减少的量。
信息增益的计算公式为:
$$\text{Information Gain}(X, Y) = H(X) - H(X|Y)$$
其中:
- ( H(X) ) 是 ( X ) 的熵,表示在没有考虑任何特征的情况下 ( X ) 的不确定性。
- ( H(X|Y) ) 是 ( X ) 在已知 ( Y ) 的条件下的条件熵,表示在已知特征 ( Y ) 的情况下 ( X ) 的不确定性。
信息增益越大,特征 ( Y ) 对于目标变量 ( X ) 的分类结果的贡献越大,因此选择信息增益大的特征作为决策树的节点。
例题
好的,我们来考虑一个简单的信息增益例题。
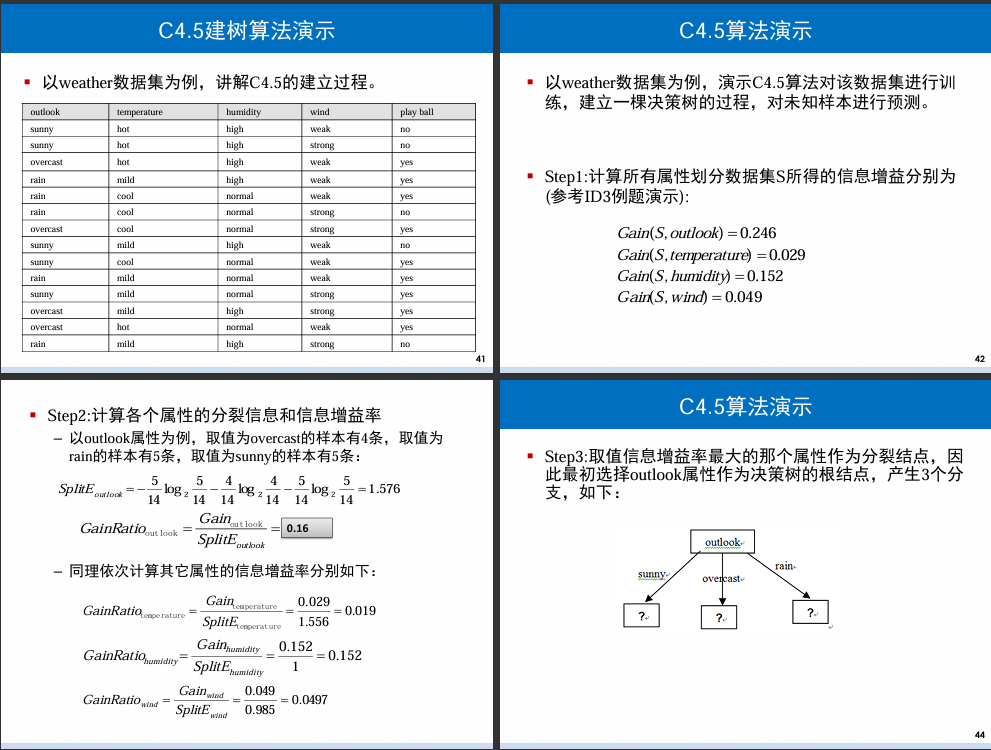
假设有一个天气数据集,包含以下四个样本,每个样本包含两个特征:”Outlook”(天气状况)和”Play”(是否进行户外活动)。我们想要根据”Outlook”特征来预测”Play”。
| Outlook | Temperature | Humidity | Windy | Play |
|---|---|---|---|---|
| Sunny | Hot | High | False | No |
| Sunny | Hot | High | True | No |
| Overcast | Hot | High | False | Yes |
| Rainy | Mild | High | False | Yes |
| Rainy | Cool | Normal | False | Yes |
| Rainy | Cool | Normal | True | No |
步骤:
计算总熵 ( H(Play) ):
首先,计算”Play”的总熵。”Play”有两种可能的值:”Yes”和”No”。
- Yes: 3 次
- No: 3 次
- 总样本数: 6
$$H(Play) = -\left(\frac{3}{6} \log_2 \frac{3}{6} + \frac{3}{6} \log_2 \frac{3}{6}\right)$$
计算得:
$$H(Play) = -\left(\frac{1}{2} \log_2 \frac{1}{2} + \frac{1}{2} \log_2 \frac{1}{2}\right) \approx 1$$
计算条件熵 ( H(Play|Outlook) ):
对于每个”Outlook”值,计算”Play”的条件熵。
- Sunny: 2 次 No,0 次 Yes 总数 2 次
- Overcast: 1 次 Yes,0 次 No 总数 1 次
- Rainy: 2 次 Yes,1 次 No 总数 3 次
$$H(Play|Outlook=Sunny) = -\left(1 \log_2 1 + 0 \log_2 0\right) = 0 $$
$$H(Play|Outlook=Overcast) = -\left(1 \log_2 1 + 0 \log_2 0\right) = 0$$
$$H(Play|Outlook=Rainy) = -\left(\frac{2}{3} \log_2 \frac{2}{3} + \frac{1}{3} \log_2 \frac{1}{3}\right) \approx 0.918$$
然后,根据”Outlook”的概率计算加权平均条件熵:
$$H(Play|Outlook) = \frac{2}{6} \times 0 + \frac{1}{6} \times 0 + \frac{3}{6} \times 0.918 \approx 0.459$$
计算信息增益 ( IG(Play, Outlook) ):
$$IG(Play, Outlook) = H(Play) - H(Play|Outlook)$$
$$IG(Play, Outlook) = 1 - 0.459 \approx 0.541$$
结论:
根据计算,”Outlook”特征的信息增益为 0.541。这意味着使用”Outlook”作为决策树的节点可以显著降低”Play”的不确定性。
3.分类算法
3.1 分类步骤
- 把数据集划分成两个部分(
训练集&测试集) - 利用训练集训练出一个模型
- 将测试集的数据对模型进行测试和反馈,评估是否合格
- 合格的话就可以将模型
投入生产使用
3.2 决策树
首先要搞懂三个概念
决策节点: 待选择的属性分支: 做出的选择(属性值)叶节点: 最终结果的标号(可能从多个分支得到)

- 一般来说,越靠近根部的(属性)节点,信息量越大,效率越高,越便于分类
- 结果不会被节点之间相互顺序影响,具体可以参考多重
if-else嵌套结构
3.3 ID3 分类算法(构建决策树)
- ID3 分类算法以
信息增益为标准构建决策树(寻找最优划分属性是决策树算法的关键) - 信息熵,就是用来描述一个属性的混乱程度


- 信息增益,就是一个随机变量有多个属性,其中一个属性已知,可以减少多少变量的不确定性(减少多少信息熵),这就是信息增益


ID3算法就是将每一个属性的信息增益算出来,将高的排在根部
缺点
只考虑深度,不考虑广度,假如所有属性带来的信息增益一样,则同一深度分支过多,决策树同样复杂
无法直接处理连续型数值(如工资数据集 110 120 134 155 171 等),必须分类之后再决策
例题
决策树之——ID3算法及示例 - hello_nullptr - 博客园
注意
所谓的递归计算,就是在选出某个根节点A之后, 根据A的不同属性的值划分
新的子数据集,重新计算该分支的总熵值例如同为A1的数据有6个,按分类结果yes有2个,no有4个
- H(A=A1) = -(2/6 * log2/6 + 4/6 * log4/6)
- 在求其它属性的信息增益
- 省略…
3.4 C4.5 算法
c4.5 处理连续型数值
- 把连续型数据离散化
- 递增排序
- 每相邻两个值的中点做分裂点,把数据集分为
S_L和S_R(左边和右边) - 求这个点的分裂信息量,100 个数据要求 99 个分裂点的信息量
分裂信息量
分裂信息(Split Information)是指在选择一个属性进行数据划分时,由于该属性的不同取值导致数据集分裂成多个子集所需要的信息量。在决策树算法中,分裂信息通常与信息增益率的计算相关。
分裂信息的计算公式可以表示为:
分裂信息计算的是,如果按照属性 ( A ) 划分数据集,需要多少位来编码表示每个样本属于哪个子集。这个值越小,表示使用属性 ( A ) 进行划分后得到的子集分布越均匀,分裂信息越小。
在 C4.5 算法中,分裂信息用于计算信息增益率(Gain Ratio),信息增益率是信息增益与分裂信息的比值,用于选择最优的属性进行数据集的划分。信息增益率的计算可以减少属性值数量较多时对信息增益的影响,从而避免选择那些具有许多值的属性。
例题
3.5 CART 算法
纯度作为构建二叉决策树的标准
在分类算法中,基尼指数通常用于决策树算法,如CART(Classification and Regression Trees)中的分类决策树构建。基尼指数用于衡量数据集的不纯度,即数据集中各类别分布的不均匀程度。基尼指数越小,表示数据集的不纯度越低,即数据集中的样本更加均匀。
基尼指数的计算方法
对于一个数据集,基尼指数的计算步骤如下:
确定类别:
确定数据集中所有可能的类别 $$ C_1, C_2, …, C_k $$ 。计算每个类别的频率:
对于每个类别$$C_i$$,计算它在数据集中的频率$$p_i$$,即$$p_i = \frac{n_i}{N}$$ ,其中$$ n_i $$ 是类别 $$ C_i$$ 中的样本数,$$ N$$ 是总样本数。计算基尼指数:
使用以下公式计算基尼指数$$G$$:
$$G = 1 - \sum_{i=1}^{k} p_i^2$$其中 $$ k $$ 是类别的总数,$p_i$ 是类别 $C_i$ 的频率。
基尼指数在分类算法中的应用
在构建决策树时,基尼指数用于选择最佳的分裂属性。算法会计算每个可能的分裂属性的基尼指数,并选择使得基尼指数最小化的属性进行分裂。这样,每次分裂都旨在最大化数据集的纯度,即减少不纯度。
示例
假设有一个简单的数据集,包含两个类别,类别A和类别B,其频率如下:
- 类别A:60% $$ p_A = 0.6 $$
- 类别B:40% $$ p_B = 0.4 $$
基尼指数计算如下:
$$
G总 = 1 - (p_A^2 + p_B^2) = 1 - (0.6^2 + 0.4^2) = 1 - (0.36 + 0.16) = 1 - 0.52 = 0.48
$$
这个基尼指数值表示当前数据集的不纯度为0.48,相对较高,意味着数据集中的样本分布不够均匀。在决策树构建过程中,我们会寻找能够最大程度降低基尼指数的属性来进行分裂,以提高树的分类能力。
例题
手动使用CART算法构建决策树涉及到选择最佳分割特征和计算不纯度。在这个例子中,我们将使用基尼不纯度(Gini impurity)作为不纯度的度量。基尼不纯度的计算公式为:$$ Gini(p) = 1 - \sum_{i=1}^{n} p_i^2 $$
其中,$ p_i $ 是第 $i $ 类的概率。
步骤 1: 计算初始不纯度
首先,我们计算整个数据集的基尼不纯度。数据集中有2条“是鱼”和3条“不是鱼”。
$$ Gini(\text{总体}) = 1 - (0.4^2 + 0.6^2) = 1 - (0.16 + 0.36) = 0.48 $$
步骤 2: 选择最佳分割特征
我们检查每个特征的每个可能的分割点,计算分割后的基尼不纯度。
特征:“是否用鳃呼吸”
- 分割为两组:用鳃呼吸(2个样本,都是鱼),不用鳃呼吸(3个样本,都不是鱼)。
- 基尼不纯度:$$ Gini(\text{用鳃呼吸}) = 0$$(因为都是鱼)
- $$Gini(\text{不用鳃呼吸}) = 0$$(因为都不是鱼)
- 加权平均基尼不纯度:$$ 0.4 \times 0 + 0.6 \times 0 = 0 $$
特征:“有无鱼鳍”
- 分割为两组:有鱼鳍(4个样本,2个是鱼,2个不是鱼),无鱼鳍(1个样本,不是鱼)。
- $$ Gini(\text{有鱼鳍}) = 1 - (0.5^2 + 0.5^2) = 0.5 $$
- $$ Gini(\text{无鱼鳍}) = 0 $$
- 加权平均基尼不纯度:$$ 0.8 \times 0.5 + 0.2 \times 0 = 0.4 $$
步骤 3: 选择最佳分割
根据计算,”是否用鳃呼吸”作为分割特征可以完全分离数据,基尼不纯度为0,这是最佳选择。
步骤 4: 构建决策树
- 根节点:是否用鳃呼吸?
- 是:是鱼(叶节点)
- 否:不是鱼(叶节点)
3.6 决策树算法总结
- 其中 ID3 只能用作分类,划分准则是信息增益。
- C4.5 也只能用作分类,划分准则是先寻找信息增益大于均值的,然后再根据增益率选择最优划分属性
- CART 决策树既可以分类也可以回归。分类时使用的基尼指数,回归时使用误差平方和。
决策树算法ID3/C4.5/CART手算案例_id3算法例题-CSDN博客
3.7 贝叶斯分类算法
- 贝叶斯分类方法是一种
基于统计的学习方法,是利用概率统计知识进行学习分类的方法 - 贝叶斯分类算法是建立在
贝叶斯定理基础上的算法
贝叶斯定理

贝叶斯定理是在H、X的先验概率P(H)、P(X)和X的后验概率P(X|H)已知的情况下,计算H的后验概率P(H|X)的方法
例题
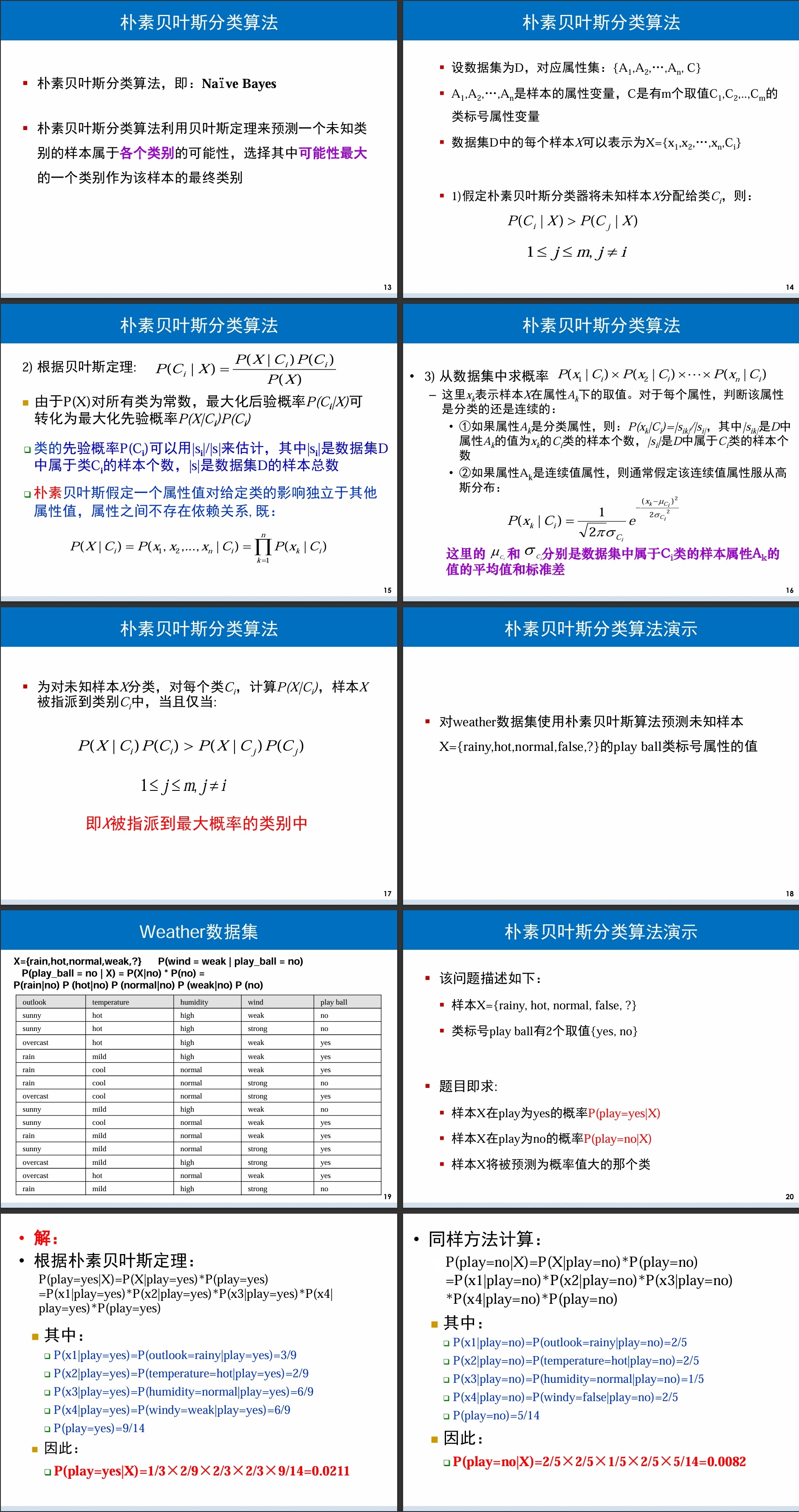
朴素贝叶斯分类
朴素贝叶斯分类算法利用贝叶斯定理来预测一个未知类别的样本属于各个类别的可能性,选择其中可能性最大的一个类别作为该样本的最终类别
上题中因为 P(X)在分母位置相同, 可以不写
朴素贝叶斯分类的优缺点
- 朴素贝叶斯分类算法的优点在于:
容易实现- 在大多数情况下所获得的结果比较好。
- 缺点:
- 算法成立的前提是
假设各属性之间互相独立。 - 当数据集满足这种独立性假设时,分类准确度较高。 而实际领域中,数据集可能并不完全满足独立性假设
- 算法成立的前提是
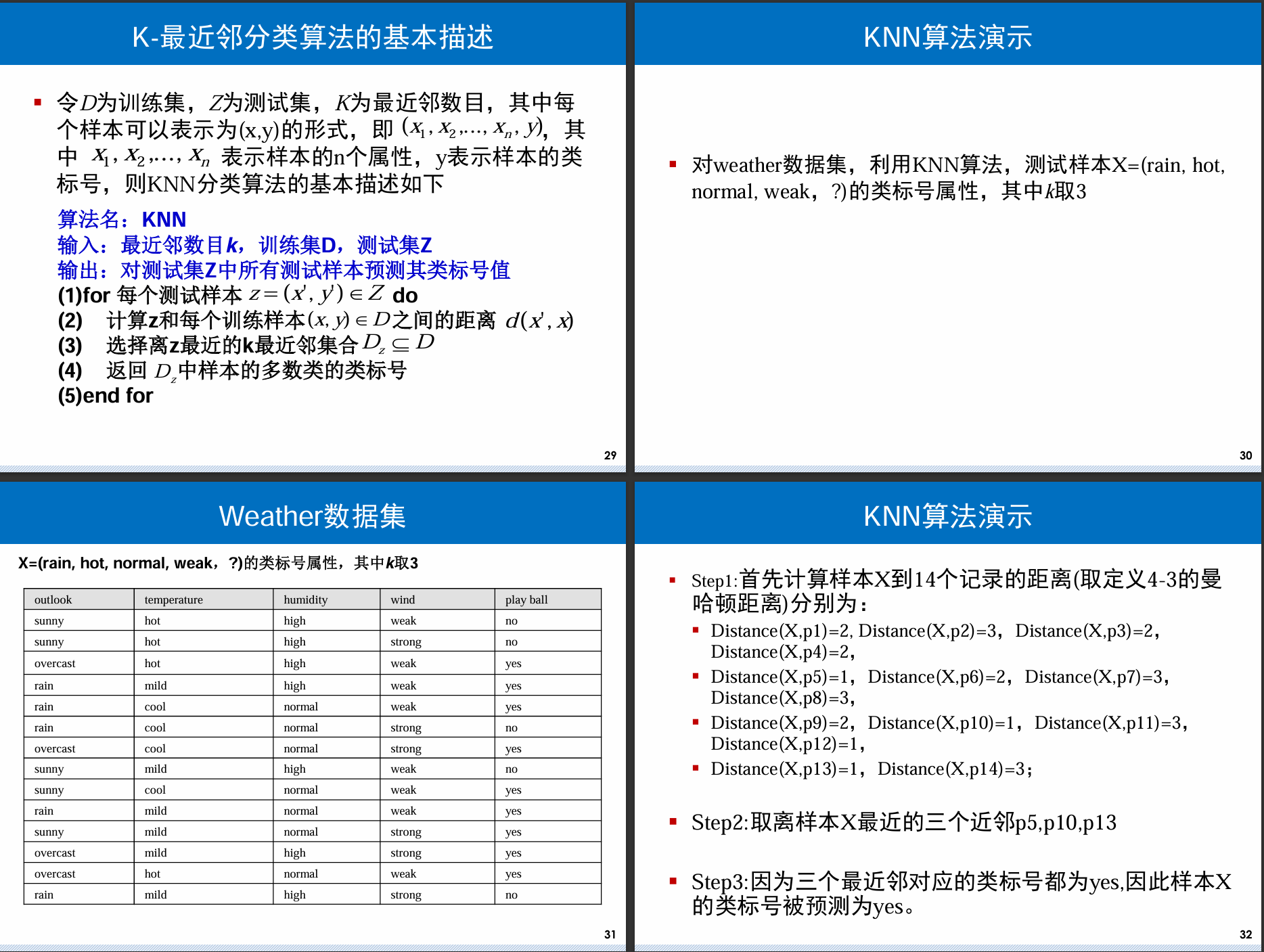
3.8 k最近邻算法
K最近邻(k Nearest Neighbors,简称KNN)方法是一种基于实例(已有样本)进行推理的算法,通过对已有训练样本集和新进的未知样本的比较得出该新进样本的类别。
它不需要先使用训练样本进行分类器的设计,而是直接用训练集对数据样本进行分类, 确定其类别标号
基本思想
K-最近邻算法的基本思想是:
对于未知类标号的样本,按照欧几里得距离找出它在训练集中的 k 个最近邻,将未知样本赋予 k 最近邻中出现次数最多的类别号
对于类别数据来说,相同为0,不同为1
4.测试和评价分类模型的方法
4.1 保持方法
- 保持(Hold Out)方法是我们目前为止讨论准确率时默认的方法
其执行步骤如下:
- 把数据集分为两个相互独立的子集:训练集和测试集。
通常情况下,指定不小于三分之二的数据分配到训练集,其余三分之一分配到测试集。 - 使用训练集来训练构建分类模型,用测试集来评估分类模型的分类效果
4.2 随机子抽样
4.3 k 折交叉验证
4.4.评价方法
5.聚类算法
博客链接
聚类是一种机器学习技术,它涉及到数据点的分组。给定一组数据点,我们可以使用聚类算法将每个数据点划分为一个特定的组。理论上,同一组中的数据点应该具有相似的属性和/或特征,而不同组中的数据点应该具有高度不同的属性和/或特征。聚类是一种无监督学习的方法,是许多领域中常用的统计数据分析技术。
5.1 聚类算法的分类
- 基于距离的聚类算法:基于距离的聚类算法是指根据数据的距离来进行聚类。常见的基于距离的聚类算法有 K-means、DBSCAN、EM 算法等。
- 基于密度的聚类算法:基于密度的聚类算法是指根据数据的密度来进行聚类。常见的基于密度的聚类算法有谱聚类、高斯混合聚类等。
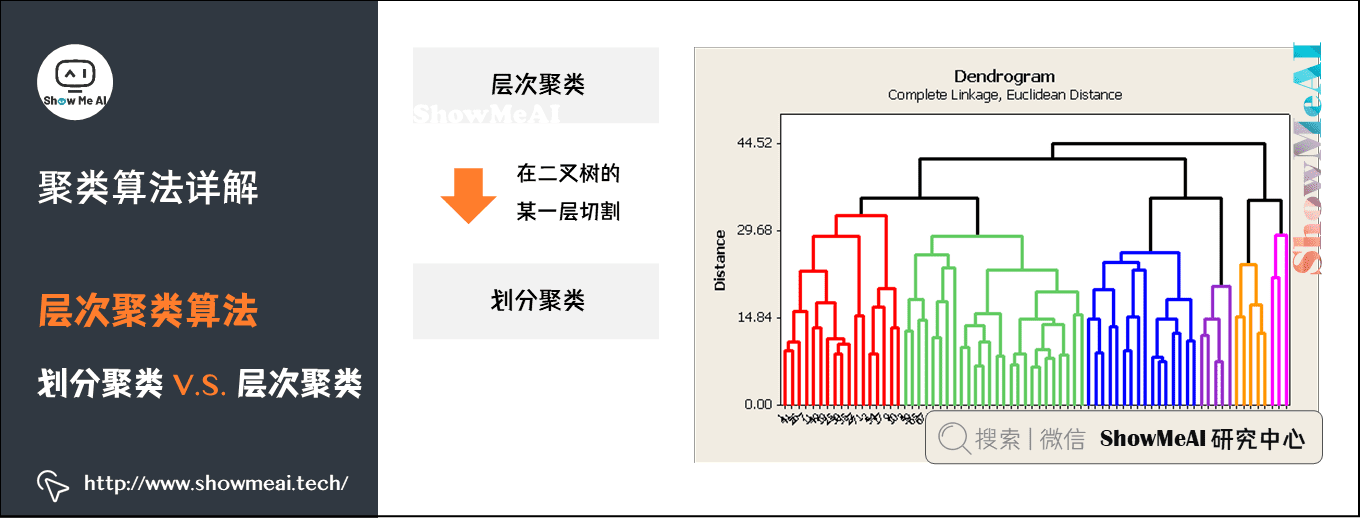
5.2 层次聚类 VS 划分聚类
图解机器学习算法(13) | 聚类算法详解(机器学习通关指南·完结)_机器学习算法教程-CSDN 博客
划分聚类得到的是划分清晰的几个类,而层次聚类最后得到的是一个树状层次化结构。
从层次化聚类转换为划分聚类很简单,在层次化聚类的某一层进行切割,就得到 1 个划分聚类。如下图所示:
5.3 K-means 聚类算法
K-means 聚类算法是一种基于距离的聚类算法,它是一种迭代算法,通过不断地将数据点分配到离它最近的中心点来实现聚类。
算法流程
K-means 聚类算法的步骤如下:
- 随机选择 k 个中心点
- 计算每个数据点到 k 个中心点的距离
- 将每个数据点分配到离它最近的中心点
- 重新计算每个中心点的位置
- 重复步骤 2-4,直到中心点不再移动
K-means 聚类算法的优点:
- 简单、快速
- 容易理解
- 结果具有全局最优解
K-means 聚类算法的缺点:
初始中心点的选择对结果影响很大- 可能收敛到局部最优解
- 计算量大
5.4 一趟聚类简介
一趟聚类算法是由蒋盛益教授提出的无监督聚类算法,该算法具有高效,简单的特点。数据集只需要遍历一遍即可完成聚类。算法对超球状分布的数据有良好的识别,对凸型数据分布识别较差。 一趟聚类可以在大规模数据,或者二次聚类中,或者聚类与其他算法结合的情况下,发挥其高效,简单的特点
算法流程
- 初始时从数据集读入一个新的对象
- 以这个对象构建一个新的簇
- 若达到数据集末尾,则转 6,否则读入一个新的对象;计算它与每个已有簇之间的距离,并选择与它距离最小的簇
- 若最小距离超过给定的阈值 r,转 2
- 否则将对象并入该簇,并更新簇心,转 3
- 结束
距离公式可以选择欧几里得距离、曼哈顿距离、切比雪夫距离等。
一趟聚类算法的优点:
- 简单、快速
- 容易理解
- 结果具有全局最优解
一趟聚类算法的缺点:
- 可能收敛到局部最优解
- 计算量大
聚类特征 CF
聚类特征(Clustering Feature,简称CF)是 BIRCH 算法中用于描述和概括数据簇的关键概念。在 BIRCH 算法中,每个聚类特征 CF 是一个三元组,可以用(N,LS,SS)表示:
- N:代表这个 CF 中拥有的
样本点的数量。 - LS(Linear Sum):代表这个 CF 中拥有的样本点
各特征维度的和向量。如果有一个 CF 包含了若干个 D 维的数据点,那么 LS 就是这些数据点在每个维度上值的总和。(线性和) - SS(Squared Sum):代表这个 CF 中拥有的样本点
各特征维度的平方和。它计算的是每个数据点在每个维度上的值的平方和。
聚类特征树(Clustering Feature Tree,简称 CF Tree)是 BIRCH 算法中用于存储和管理聚类特征的数据结构。CF 树的每个节点由若干个聚类特征 CF 组成,内部节点的 CF 有指向孩子节点的指针,所有的叶子节点用一个双向链表链接起来。CF 树的构造是 BIRCH 算法的核心,它允许算法在单遍扫描数据集的情况下进行有效的聚类。
CF 具有线性关系的性质,即 CF1+CF2=(N1+N2,LS1+LS2,SS1+SS2),这个性质使得在 CF 树中,父节点的 CF 可以通过其所有子节点的 CF 值相加得到,从而高效地更新 CF 树。这种设计使得 BIRCH 算法特别适合于处理大规模数据集,并且能够快速识别出数据集中的异常值。
5.5 基于密度的 DB-SCAN 算法
DB-SCAN 算法中,把样本点分为三类
- 核心点: 其邻域内点的数量大于或等于
MinPts - 边界点: 非核心点,但是
落在某个核心点的邻域内 - 噪声点: 既非核心点也非边界点
样本点之间的关系
- 直接密度可达(directly density-reachable: 两个点必须是核心点,若
点x_i位于点x_j的邻域中,则称x_i由x_j直接密度可达 - 密度可达(density-reachable): 对 x_i 与 x_j,若存在
样本序列p1,p2,……,pn,其中 p_1=x_i,p_n=x_j;且 p_i+1 由 p_i 密度直达,则称x_j由x_i密度可达。 - 密度相连: 对于 x_i 和 x_j,
若存在一点k使得x_i 和 x_j均由点k密度可达,则称 x_i 和 x_j 密度相连
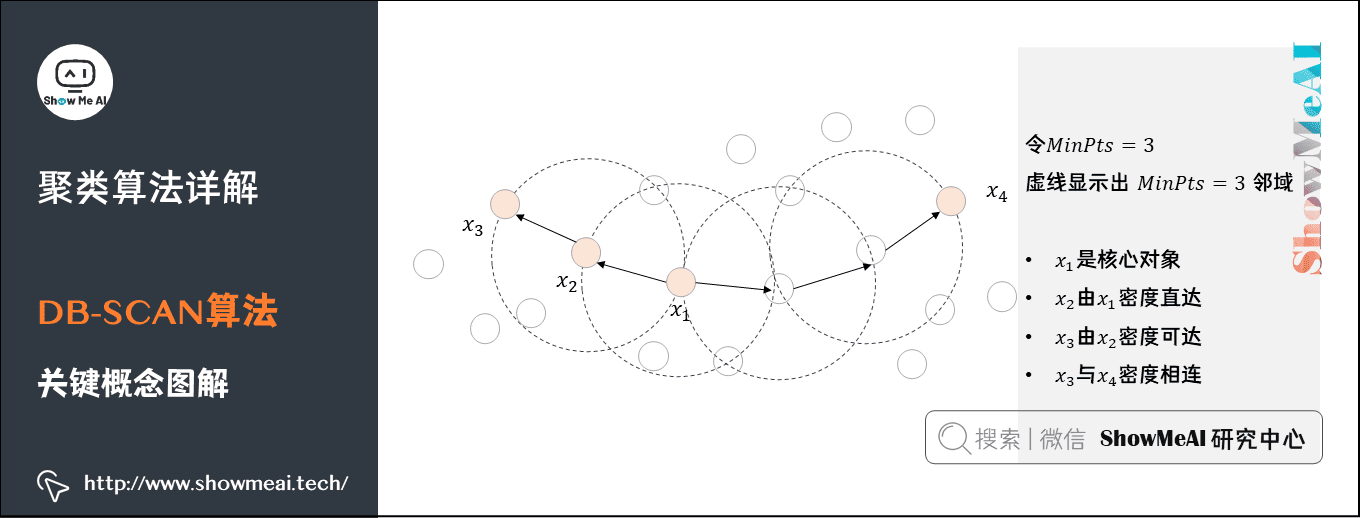
先假设要求的最小点密度MinPts是3.
- x1, x2, x3, x4 都是核心点(
邻域内点数>=MinPts) - x1 与 x2
处于一个邻域,所以二者是密度直达的关系,而 x3 与 x2 也是密度直达的关系,通过 x2,x1 与 x3 是密度可达的关系 - x3 与 x4
通过多个核心对象(核心点)实现密度相连。
例题解析
DBSCAN 算法的一个典型例子是在一个二维平面上对一组点进行聚类。假设我们有一组二维空间中的点,我们希望根据这些点的密度来将它们分成几个簇。
假设我们有以下一组二维空间中的点:
[
(1, 1), (2, 1), (2, 2), (2, 3),
(4, 4), (5, 4), (6, 4), (7, 4),
(8, 8), (9, 8), (10, 8), (11, 8),
(12, 12), (13, 12), (14, 12)
]我们选择MinPts = 3和ε = 1.5(邻域半径)并使用Mahattan距离公式。DBSCAN 算法的步骤如下:
初始化:将所有点标记为未访问。
遍历每个点:
- 对于每个未访问的点,找到其 ε 邻域内的所有点。
- 如果邻域内的点数大于或等于
MinPts,则该点是一个核心对象。 - 以该核心对象为中心,开始聚类,将所有密度可达的点加入到同一个簇中。
聚类过程:
- 点(1, 1)的邻域内只有 2 个点,所以它不是核心对象。
- 点(2, 1)的邻域内有多于 3 个点,因此它是一个核心对象。它的邻域包括(1, 1),(2, 2)和(2, 3)。这些点都加入到同一个簇中。
- 点(2, 2)和(2, 3)的邻域也都有多于 3 个点,它们会将它们的邻域内的所有点加入到同一个簇中。这个簇最终会包括点(1, 1),(2, 1),(2, 2)和(2, 3)。
- 点(4, 4)的邻域内有多于 3 个点,它是一个核心对象。它的邻域包括(5, 4),(6, 4)和(7, 4)。这些点都加入到一个新的簇中。
- 点(8, 8)的邻域内有多于 3 个点,它是一个核心对象。它的邻域包括(9, 8),(10, 8)和(11, 8)。这些点都加入到一个新的簇中。
- 点(12, 12)的邻域内有多于 3 个点,它是一个核心对象。它的邻域包括(13, 12)和(14, 12)。这些点都加入到一个新的簇中。
结果:最终,我们得到了三个簇,以及一些噪声点。
这个例子展示了 DBSCAN 如何根据点的密度来识别簇,并且能够处理噪声点。在实际应用中,选择合适的ε和MinPts对于算法的效果至关重要。
DB-SCAN 算法的优缺点
DBSCAN 算法的优点是它不需要预先指定簇的数量,并且可以识别出噪声点。
但它也有缺点,比如对参数ε和MinPts的选择很敏感,且在处理高维数据时可能会遇到维度灾难。
5.6 基于图的 Chameleon 算法
基于图的聚类算法的特点
- 稀疏化近邻图,只保留最近邻
- 基于两个对象共享的近邻个数来定义相似性度量
- 可以发现形状和大小多样的类
- 要提供两个类合并的依据
算法介绍
Chameleon 是一种基于密度的聚类算法,它是由 Karl J. Chabassier 和 Alexandre Boudet 在 1997 年提出的。Chameleon 算法是对 DBSCAN 算法的改进,它旨在解决 DBSCAN 算法在处理不同密度区域时的一些问题。Chameleon 算法通过动态调整邻域半径来适应不同密度的区域,从而更好地识别不同密度的簇。
算法的核心思想:
动态邻域半径:Chameleon 算法不是使用固定的邻域半径(如 DBSCAN 中的 ε),而是根据每个点的局部密度动态调整邻域半径。这意味着在高密度区域,邻域半径可能较小,而在低密度区域,邻域半径可能较大。
密度适应:算法通过计算每个点的密度,并根据这些密度值来调整邻域半径,从而适应不同密度的区域。
相似性度量:Chameleon 算法使用相似性度量来确定两个点是否应该属于同一个簇。这种度量考虑了点之间的距离和它们的密度。
噪声处理:与 DBSCAN 类似,Chameleon 算法也能识别并处理噪声点。
绝对互连度和相对互连度
Chameleon 算法及 Matlab 实现_matlab chameleon 聚类算法-CSDN 博客
- RI = 公共边数和 / (两点内部边数和 * 2)
- RC = (公共边数和 /
两点点数相乘) / ((点 A 的点数 / 两点点数之和_ 点 A 的内部边数 /点A的点数的平方) + (点 B 的点数 / 两点点数之和_ 点 B 的内部边数 /点B的点数的平方))
例: 类 C1 包含 10 个点,内部边数和为 100,类 C2 包含 20 个点,内部边数和为 166,C1 和 C2 之间的边数和为 50
问: 计算:RI(C1,C2),RC(C1,C2)
- RI=50/(100+166)*2
- RC=(50/(10*20)) / (10/30(100/100)+20/30(166/400))
算法的步骤:
初始化:为每个点计算其密度,并根据密度动态确定邻域半径。
构建相似性图:根据点之间的相似性度量构建一个相似性图,其中边代表相似的点对。
谱聚类:使用谱聚类技术对相似性图进行聚类,以识别簇的边界。
合并相似的簇:根据相似性度量合并那些相似度较高的簇。
迭代优化:迭代地调整邻域半径和相似性度量,直到聚类结果稳定。
优点和缺点
优点:
- 适应不同密度:能够适应不同密度的区域,更好地识别不同密度的簇。
- 灵活性:通过动态调整邻域半径和相似性度量,算法具有较高的灵活性。
- 噪声鲁棒性:能够识别并处理噪声点。
缺点:
- 计算复杂度:由于需要动态调整邻域半径和进行谱聚类,算法的计算复杂度较高。
- 参数选择:虽然算法减少了对参数的依赖,但仍然需要用户指定一些参数,如密度计算方法。
Chameleon 算法适用于那些数据点密度不均匀的场景,它通过动态调整邻域半径和使用谱聚类技术,提高了聚类的效果和鲁棒性。然而,由于其较高的计算复杂度,它可能不适用于大规模数据集。
6.关联规则挖掘
6.1 算法定义
- 关联规则挖掘用于发现隐藏在大型数据集中的令人感兴趣的联系,所发现的模式通常用关联规则或频繁项集的形式表示。
- 关联规则反映了一个事物与其他事物之间的相互依存性和关联性。
- 如果两个或多个事物之间存在一定的关联关系,那么,其中一个事物发生就能够预测与之相关联的其他事情的发生。
- 关联规则挖掘用于知识发现,而非预测,所以是属于
无监督的机器学习算法。
6.2 经典例子
沃尔玛在对商品销售数据进行数据挖掘分析时,发现啤酒和尿布经常被一起购买,这个关联关系的原因在于:过来买啤酒的爸爸总是会顺手再买尿布。将两者货架摆放在一起,其销量果然上升。
关联规则挖掘算法不仅被应用于购物篮分析,还被广泛的应用于网页浏览偏好挖掘,入侵检测,连续生产和生物信息学领域。
6.3 相关概念
项集:包含0个或多个项的集合,如包含 k项称为 k-项集, 上面的(啤酒,尿布)就是一个二项集共现关系:指项集中两项同时出现的关系, 例如例子中的 啤酒和尿布事务T与事务集D:- 一个事务T就是一个项集,每一个事务T均与一个唯一标识符Tid相联系。
- 不同的事务一起组成了事务集D,它构成了关联规则发现的事务数据库个数。
- 上边的例子中,每个顾客的一袋子商品(所有商品放到一个袋子里面)就是一个事务,那么以每个袋子单位,今天的销售量就是一个事务集。
支持度计数(Support count): 指包含特定项集的事务个数,用符号 σ 表示,如 σ({milk,beer,bread})=2 ,表示今天同时有买个这3种商品的人次有2个。
支持度:指包含特定项集的事务数与总事务数的比值,用符号 s 表示,如 s({milk,beer,bread})=2/5 ,表示今天有2/5的顾客一次性同时购买了这3种商品。频繁项集(Frequent Itemset): 支持度 >=minsup的项集,(满足最小支持度阈值minsup)关联规则:
关联规则是指形如 X→Y 的蕴含表达式,其中X和Y是不相交的项集。如{milk,diaper}和{beer}。置信度(Confidence): 指包含指定{X,Y}的事务数与包含{X}的事务数的比值,用符号 c 表示. 表示当A项出现时B项同时出现的频率,记作 c {A→B}。换言之,置信度指同时包含A项和B项的交易数与包含A项的交易数之比。
| Tid | Items |
|---|---|
| 1 | bread,milk |
| 2 | bread,disper,beer,eggs |
| 3 | milk,disper,beer,coke |
| 4 | bread,milk,disper,beer |
| 5 | bread,milk,disper,coke |
X = {milk,diaper}, Y = {beer},求关联规则 X→Y 。
支持度 s({milk,diaper,beer})=2/5 ,
置信度 c({milk,diaper,beer})=σ({milk,diaper,beer}) / σ({milk,diaper}) = 2 / 3
关联规则挖掘问题是指给定事务的集合T,关联规则发现是指找出支持度大于等于minsup并且置信度大于等于minconf的所有规则,minsup和minconf是对应的支持度和置信度。
| Tid | 项集 |
|---|---|
| 10 | A,B,C |
| 20 | A,C |
| 30 | A,D |
| 40 | B,E,F |
其中有以下
| 指定项集 | 支持度 |
|---|---|
| {A} | 75% |
| {B} | 50% |
| {C} | 50% |
| {A, C} | 50% |
给定最小支持度minsup为50%,最小置信度minconf为50%,挖掘关联规则 A→C .
支持度= support({A}&{C}) = 50%
置信度= σ({A}∪{C})σ({A}) = 2/3
指定关联规则挖掘成功。
6.4 挖掘关联规则(Mining Association Rules)
大多数关联规则挖掘算法通常采取的一种策略是,将关联规则挖掘任务分解成如下两个主要的子任务:
1、频繁项集产生(Frequent Itemset Generation):
任务目标是发现满足最小支持度阈值的所有项集,这些项集称为频繁项集。
2、规则的产生(Rule Generation):
任务目标是从上一步发现的频繁项集中提取所有高置信度的规则,这些规则称为强规则(Strong Rule)。
6.5 Apriori算法
寻找频繁项集的常用算法。
先验原理:
1、如果一个项集是频繁的,则它的所有子集也一定是频繁的;
2、相反,如果一个项集是非频繁的,那么它的所有超集也是非频繁的。
存在项集{A,B},包含它的就是超集,如{A,B,C}.
此原理的作用在于,如果一个项集被发现是非频繁的,可以将其子集或者超集提前剪除掉,降低计算开销。
Apriori算法工作原理:
原始表,给定最小支持度计数为2。
| Tid | 项集 |
|---|---|
| 10 | A,C,D |
| 20 | B,C,E |
| 30 | A,B,C,E |
| 40 | B,E |
第一步,k=1,计算一项集的支持度计数。
| Itemset | support count |
|---|---|
| {A} | 2 |
| {B} | 3 |
| {C} | 3 |
| {D} | 1 |
| {E} | 3 |
方法:直接数数项集在原始表出现的次数。
可见,项集{D}的支持度计数小于2,由先验原理,凡是包含{D}的都可以不管不顾,故可提前剪除掉(剪枝)。
上表就变成了如下表格。
| Itemset | support count |
|---|---|
| {A} | 2 |
| {B} | 3 |
| {C} | 3 |
| {E} | 3 |
第二步,k=2,计算二项集的支持度计数。
二项集就是把一项集两两连接。
| Itemset | support count |
|---|---|
| {A,B} | 1 |
| {A,C} | 2 |
| {A,E} | 1 |
| {B,C} | 2 |
| {B,E} | 3 |
| {C,E} | 2 |
跟上一步一样,看着原始表数数即可。
剪除掉支持度计数小于2的项集后,可得表格。
| Itemset | support count |
|---|---|
| {A,C} | 2 |
| {B,C} | 2 |
| {B,E} | 3 |
| {C,E} | 2 |
第三步,k=3,计算三项集的支持度计数。
三项集及其以上项集的连接遵循以下规则:
{A,C}与{B,C}连接,两个项集的尾项划掉,剩余项不同,不可连接。
{B,C}与{B,E}连接,两个项集的尾项划掉,剩余项相同,可连接,成{B,C,E}。
逐一连接,可得。
| Itemset | support count |
|---|---|
| {B,C,E} | 2 |
第四步,k=4,计算四项集的支持度计数。
但是四项集为空,算法流程终止,第三步的频繁项集为最终结果。
综上,Apriori算法的工作原理是一个递归过程:
k=1,计算一项集的支持度计数;
根据给定的最小支持度计数筛选出k项集的频繁项集;
k-1项集两两连接形成k项集,如果为空,则上一步就是最终结果;
计算k项集的支持度计数;
根据给定的最小支持度计数筛选出k项集的频繁项集;
k=k+1,重复3-5步。
算法优缺点
Apriori算法特点:
多次扫描数据库;
候选项规模庞大;
计算支持度开销大。
Apriori算法缺点在于,需要反复的生成候选项,如果项的数目比较大,候选项的数目将达到组合爆炸式的增长。
针对于此,另一种发现频繁项集的算法:FP-Growth算法,可以避开这个缺点。
Apriori算法利用先验原理逐步减少候选集的数量,FP-Growth算法则利用先验原理和生成FP-Tree相结合来减少比较的次数。
FP-Growth算法的平均效率远高于Apriori算法。
6.6 关联规则挖掘过程
在挖掘出频繁项集之后,再利用频繁项集生成关联规则,具体步骤如下:
先给定最小置信度。
1、根据每个频繁项集,找到它所有的非空真子集。
2、根据这些非空真子集,两两组成所有的关联规则。
3、计算所有的关联规则的置信度,移除小于最小置信度的规则,得到强关联规则。
注意,如果一个频繁项集是{A,B},那么可能的一个关联规则是 A→B ,说明某人买了A,大概率也会买B,但顺序反过来是不成立的。
具体栗子可参考 极相 空林玄一:【理论】挖掘关联规则 。
7.离群因子检测
下面是三种基于距离、密度、聚类的离群点检测方法的原理:
1. 基于距离的离群点检测方法
原理:
- 核心思想:基于距离的离群点检测方法认为,如果一个数据点与其它数据点的距离较远,则可能是一个离群点。
- 距离度量:通常使用欧氏距离、曼哈顿距离等来度量数据点之间的距离。
- 阈值设定:设定一个距离阈值,超过该阈值的数据点被认为是离群点。
- 聚类质心:在聚类算法中,每个聚类的质心(或称为中心点)代表了该聚类的特征位置。数据点到质心的距离可以作为判断其是否为离群点的依据。
import numpy as np
# 假设data是一个包含所有数据点的numpy数组
# 计算每个点到质心的距离
def calculate_distances(data, centroids):
distances = []
for point in data:
distances.append(min(np.linalg.norm(point - centroid) for centroid in centroids))
return np.array(distances)
# 设定阈值
threshold = 10
distances = calculate_distances(data, centroids)
outliers = data[distances > threshold]2. 基于密度的离群点检测方法
原理:
- 核心思想:基于密度的方法认为,离群点通常位于低密度区域,而正常点位于高密度区域。
- 局部密度:计算数据点的局部密度,即在一定半径或邻域内的数据点数量。
- 相对密度:比较数据点的密度与其邻近点的密度,如果某个点的密度显著低于其邻近点,则可能是离群点。
- 局部离群因子(LOF):LOF算法通过计算数据点与其邻近点的局部密度比来确定离群点,如果比值大于1,则该点可能是离群点。
from sklearn.neighbors import LocalOutlierFactor
# 假设X是一个包含所有数据点的特征矩阵
lof = LocalOutlierFactor(n_neighbors=20, contamination=0.1)
y_pred = lof.fit_predict(X)
# 标记离群点
outliers = X[y_pred == -1]3. 基于聚类的离群点检测方法
原理:
- 核心思想:基于聚类的方法认为,离群点可能不属于任何聚类,或者属于聚类边缘的点。
- 聚类结果:通过聚类算法(如K-Means)将数据点分到不同的聚类中。
- 聚类稳定性:检查数据点在聚类中的稳定性,如果一个点经常在不同迭代中改变聚类归属,它可能是一个离群点。
- 聚类边界:离群点可能位于聚类之间的边界区域,通过分析聚类边界可以识别离群点。
- 离群因子(OF):计算每个点的离群因子,该因子反映了点与其聚类中心的距离相对于聚类内其他点的平均距离。如果一个点的OF值显著高于平均值,它可能是一个离群点。
from sklearn.cluster import KMeans
# 假设data是一个包含所有数据点的numpy数组
kmeans = KMeans(n_clusters=3, random_state=0).fit(data)
labels = kmeans.labels_
# 计算每个点的离群因子
def calculate_outlier_factor(data, labels):
unique_labels = np.unique(labels)
outlier_factor = np.zeros(data.shape[0])
for i, point in enumerate(data):
cluster_points = data[labels == labels[i]]
point_distance = np.linalg.norm(point - kmeans.cluster_centers_[labels[i]])
mean_distance = np.mean(np.linalg.norm(cluster_points - kmeans.cluster_centers_[labels[i]], axis=1))
outlier_factor[i] = point_distance / mean_distance
return outlier_factor
outlier_factors = calculate_outlier_factor(data, labels)
threshold = np.percentile(outlier_factors, 95) # 设定95百分位数为阈值
outliers = data[outlier_factors > threshold]这三种方法各有优势和适用场景,实际应用中可以根据数据的特性和需求选择合适的方法。
8.期末例题
分类例题
ID3算法
决策树之——ID3算法及示例 - hello_nullptr - 博客园

C4.5算法
决策树之——C4.5算法及示例 - hello_nullptr - 博客园
筛选的结果类似
| outlook | temperature | humidity | wind | play ball |
|---|---|---|---|---|
| sunny | hot | high | weak | no |
| sunny | hot | high | strong | no |
| sunny | mild | high | weak | no |
| sunny | cool | normal | weak | yes |
| sunny | mild | normal | strong | yes |
- 然后计算新的 H(PlayBall) ,OutLook值为sunny的共有5条.其中palyball为yes的有2条,no有3条
H(PlayBall) = - (log 2/5 * 2/5 + log 3/5 * 3/5)
IG(Temperature) = 2/5 * H(play | temp=hot) + 2/5 * H(play | temp=mild) + 1/5 * H(play | temp=cool)
= 2/5 * -(log 0/2 * 0/2 + log 2/2 * 2/2)temp=hot中有两条数据,其分类结果都为no + () + ()
然后求 SplitE(temp) = - (2/5 * log 2/5)
hot- (2/5 * log 2/5)mild- 1/5 * log 1/5cool最后求的 GainRatio(temp)
递归……
CART分类算法
机器学习之——基尼指数的计算例题 - hello_nullptr - 博客园
求熵代码
决策树熵计算程序Python+CSV格式数据集 - hello_nullptr - 博客园
聚类例题
K-means聚类算法
- 选择K值:首先,你需要确定要分成多少个簇(K值)。这通常需要一些领域知识或通过肘部法则(Elbow Method)来确定。
- 初始化中心点:随机选择K个数据点作为初始的簇中心。
- 分配数据点:将每个数据点分配到最近的簇中心,形成K个簇。
- 更新中心点:计算每个簇的平均值,并将簇中心更新为这个平均值。
- 重复步骤3和4:直到簇中心不再发生变化或达到一定的迭代次数。
- 评估聚类效果:使用轮廓系数(Silhouette Coefficient)或其他指标来评估聚类的效果。
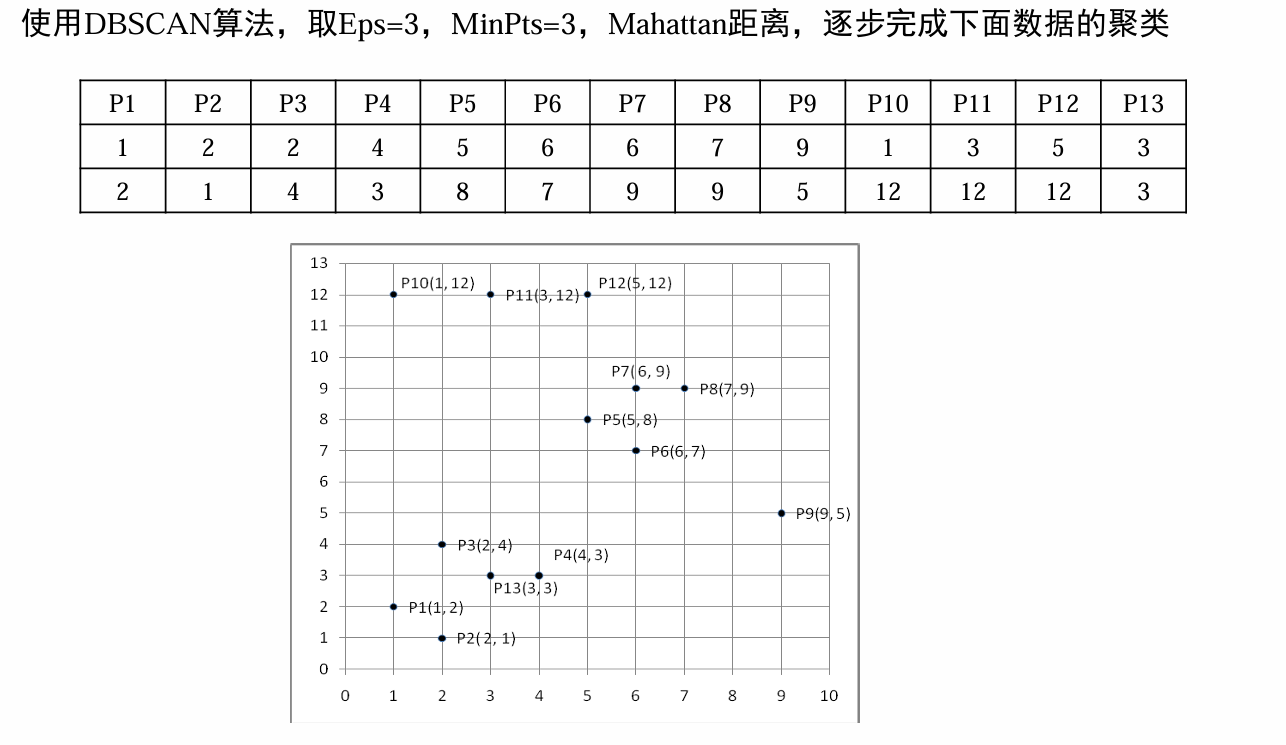
具体步骤
步骤1: 选择K=2。
步骤2: 随机选择两个点作为初始中心,比如P1(1,2)和P5(5,8)。
步骤3: 分配数据点到最近的中心。
步骤4: 更新中心点。
这个过程需要重复进行,直到中心点不再变化。由于这是一个迭代过程,我将为您展示第一轮迭代的结果。
第一轮迭代:
- 簇1中心: P1(1,2)
- 簇2中心: P5(5,8)
分配数据点:
- 簇1: P1, P2, P3, P4, P10, P11, P13
- 簇2: P5, P6, P7, P8, P9, P12
更新中心点:
- 簇1新中心: ((1+2+2+4+1+3+3)/7, (2+1+4+3+12+12+3)/7) = (2, 5.43)
- 簇2新中心: ((5+6+6+7+9+5)/6, (8+7+9+9+5+12)/6) = (6.17, 8.33)
这个过程会继续进行,直到中心点稳定下来
一趟聚类算法
- 假设 阈值r = 5
- 读入数据集第一个点作为初始的簇中心
- 读入第二个点(2, 1),计算距离为2 <= r,于是归于类别C1,并更新簇中心为 (1.5, 1.5)
- 读入第三个点(2, 4),计算距离为3 <= r,于是归于类别C1,并更新簇中心为 ((1+2+2) /3, (2+1+4)/3)
- 继续这个过程……