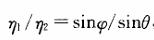第一章 绪论
计算机图形学是利用计算机研究图形的表示、生成、处理和显示的学科。
光栅图形学:其核心过程是光栅化,即将矢量图形转换为像素网格的过程。光栅就是通过一栏一栏的像素绘成图像
1.1 计算机图形学的研究内容
计算机中图形的表示方法,以及利用计算机进行图形的计算、处理和显示的相关原理与算法,构成了计算机图形学的主要研究内容。图形通常由点、线、面、体等几何元素和灰度色彩、线型、线宽等非几何属性组成。从处理技术上来看,图形主要分为两类:一类基于线条信息表示,如工程图、等高线地图和曲面的线框图等;另一类是明暗图(shading),也就是通常所说的真实感图形。
计算机图形学的一个主要目的就是要利用计算机产生令人赏心悦目的真实感图形。为此,一般先建立目标图形所描述场景的几何表示,再采用某种光照模型,计算在假想的光源.纹理、材质属性下几何模型的光照效果。
计算机图形学的研究内容非常广泛,如图形硬件、图形标准、图形交互技术、光栅图形生成算法、曲线曲面造型、实体造型、真实感图形计算与显示算法,以及科学计算可视化、计算机动画、自然景物仿真和虚拟现实等。作为一本面向计算机专业的本科生和非计算机专业的研究生的图形学教材,本书着重讨论与光栅图形生成、曲线曲面造型和真实感图形生成相关的原理与算法。
1.2 计算机图形学发展历程
1950年,第一台图形显示器作为美国麻省理工学院(MIT)旋风1号(WhirlwindⅠ)计算机的附件诞生了。该显示器用一个类似于示波器的阴极射线管(CRT)来显示一些简单的
1962年,MIT林肯实验室的 IvanE.Sutherland 发表了题为“Sketchpad:一个人机交互通信的图形系统”的博士论文,他在论文中首次使用了计算机图形学(ComputerGraphics)这个术语,证明了交互计算机图形学是一个有价值的研究领域,从而确定了计算机图形学作为一个崭新的科学分支的独立地位。
同在20世纪60年代早期,法国雷诺汽车公司的工程师 Pierre Bézier发展了一套被后人称为 Bézier 曲线、曲面的理论,成功地用于几何外形设计,并开发了用于汽车外形设计的 UNISURF 系统。Coons的方法和 Bézier的方法是 CAGD(计算机辅助几何设计)领域的开创性工作。值得一提的是,计算机图形学的最高奖是以 Coons 的名字命名的
20世纪70年代是计算机图形学发展过程中一个重要的历史时期。由于光栅显示器的诞生,早在60年代就已萌芽的光栅图形学算法便迅速发展起来。区域填充、裁剪、消隐等基本图形概念及其相应的算法纷纷诞生,图形学进人了第一个兴盛时期。
同在20世纪70年代,计算机图形学的另外两个重要进展是真实感图形学和实体造型技术的产生。1970年,Bouknight 提出了第一个光反射模型。1971年,Gourand 提出“漫反射模型十插值”的思想,被称为 Gourand 明暗处理。1975年,Phong 提出了著名的简单光照模型–Phong模型”。这些都是真实感图形学的开创性工作。1980 年,Whitted 提出了一个光透视模型--Whitted 模型,并第一次给出光线跟踪算法的范例,实现了 Whitted模型。1984年,美国 Cornell(康内尔)大学和日本广岛大学的学者分别将热辐射工程中的辐射度方法引人到计算机图形学中,成功地模拟了理想漫反射
1.3 计算机图形学的应用及研究前沿
- 计算机辅助设计与制造
- 可视化
- 真实感图形实时绘制与自然景物仿真
- 计算机动画
- 用户接口
- 计算机艺术
1.4 图形设备
高质量的计算机图形离不开高性能的计算机图形硬件设备。一个图形系统通常由图形处理器、图形输入设备和输出设备构成。
图形显示设备
彩色 CRT 显示器
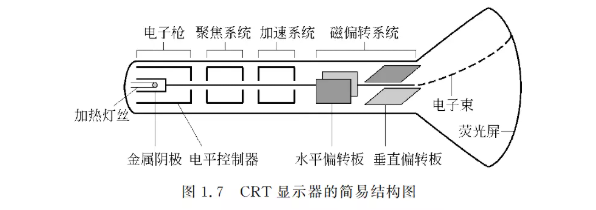
图 1.7给出了CRT的工作原理。
高速的电子東由电子枪发出,经过聚焦系统、加速系统和磁偏转系统就会到达荧光屏的特定位置。荧光物质在高速电子的轰击下会发生电子跃迁,即电子吸收能量从低能态变为高能态,由于高能态很不稳定,在很短的时间内荧光物质的电子会从高能态重新回到低能态,这时将发出荧光,屏幕上的那一点就亮了。从这种发光原理可以看出,这样的光不会持续很久,因为很快所有的电子都将回到低能态,不会再有光发出。所以要保持显示一幅稳定的画面,必须不断地发射电子束。 那么电子東是如何发出的,又是如何控制它的强弱的呢?由图1.7可以看出,电子枪由一个加热器、一个金属阴极和一个电平控制器组成。当加热器加到一定高温时,金属阴极上的电子就会摆脱能垒的束缚,进射出去。而电平控制器是用来控制电子束强弱的,当加上正电压时,电子柬就会大量通过,将会在屏幕上形成较亮的点;当控制电平加上负电压时,依据所加电压的大小,电子束被部分或全部阻截,通过的电子很少,屏幕上的点也就比较暗。
想要保持稳定图像,那么就需要不断地发射电子束。
刷新一次是指电子束从上到下将荧光屏扫描一次。只有刷新频率达到一定值后,图像才能稳定显示。大约达到60Hz时,人眼才能感觉不到屏幕闪烁,但要使人眼觉得舒服,一般必须有85Hz以上的刷新频率。
隔行扫描:能够满足扫描速度较慢的显示机器,区别于传统的逐行扫描,隔行扫描能够模拟将扫描频率加倍,但是效果比不上真正的逐行60Hz
LCD 液晶显示器
- 基本原理
液晶是一种介于液体和固体之间的特殊物质,它具有液体的流态性质和固体的光学性质。当液晶受到电压的影响时,就会改变它的物理性质而发生形变,此时通过它的光的折射角度就会发生变化,而产生色彩。液晶屏幕后面有一个背光,这个光源先穿过第一层偏光板,再来到液晶体上,而当光线透过液晶体时,就会产生光线的色泽改变。从液晶体射出来的光线,还必须经过一块彩色滤光片以及第二块偏光板。由于两块偏光板的偏振方向成90°,再加上电压的变化和一些其他的装置,液晶显示器就能显示想要的颜色了。
图形处理设备
一个光栅显示系统离不开图形处理器,图形处理器是图形系统结构的重要元件,是连接计算机和显示终端的纽带,可以说有显示系统就有图形处理器(俗称显卡)。
图形输入设备
| 设备名称 | 用途描述 |
|---|---|
| 键盘 | 用于录入文本、发布命令和选择菜单项等。 |
| 鼠标 | 通过移动和点击来控制光标位置和进行操作。 |
| 光笔 | 通过光电技术检测屏幕上的位置,用于图形绘制和标记。 |
| 数字化仪 | 用于绘画着色或交互式选择坐标位置,可输入二维或三维空间的坐标值。 |
| 触摸板 | 通过手指触摸来控制光标移动和进行操作。 |
| 图形扫描仪 | 将纸质文档或图像扫描成数字格式,以便计算机进行处理和存储。 |
| 手写输入板 | 用于手写输入,将手写笔迹转换为数字信号。 |
| 语音输入设备 | 通过语音识别技术将语音转换为文本或命令。 |
| 数据手套 | 用于动作捕捉,让计算机识别手部运动,常用于虚拟现实系统。 |
| 操纵杆 | 用于游戏或模拟操作,通过物理按钮和操纵杆与计算机交互。 |
| 按钮盒和旋钮 | 按钮和开关常用来输入预定的功能,旋钮用于输入标量值。 |
| 三维扫描仪 | 用于捕捉物体的三维形状和深度信息,常用于3D建模和仿真。 |
| 深度相机 | 用于捕捉物体的深度信息,提供三维感知能力。 |
| 光穹 | 一种高精度的三维扫描设备,用于在光学条件下捕捉物体的完整三维信息。 |
1.5 最新研究方向
绘制:
- 表面几何细节实时绘制
- 半透明材质实时编辑
- 动态场景实时绘制
视频:
- 视频补全
几何:
- 拓扑结构自动修复
- 积分不变量技术
第二章 二维变换
2.1 向量
什么是向量? 我们所使用的所有点和向量都是基于某一坐标系定义的。

从几何的角度看,向量是具有长度和方向的实体,但是没有位置。而点是只有位置,没有长度和方向
向量表示一个点到另一个点的位移。假设在XoY直角坐标系中,一个向量可以由它的不同方向的分量表示。
向量的基本操作
- 向量
相加减: 向量(2, 6) + 向量(3, 1) = (5, 7) - 标量的
数乘: 3 * 向量(1,4) = (3, 12)

向量线性组合:掌握了向量的加法和数乘,就可以定义任意多个向量的线性组合

- 有两种特殊的线性组合在计算机图形学中很重要
- 仿射组合:
线性组合的系数之和=1,a1 + a2 + a3 + … + an = 1 凸组合:在仿射组合的基础上,还要求每个系数>0
- 仿射组合:
- 点乘和叉乘
代数公式和几何公式实际上是等价的,它们从不同的角度描述了同一个数学概念。


余弦定理:用一个向量来描述一篇新闻,
当夹角的余弦接近于1时,两条新闻相似,从而可以归成一类;夹角的余弦越小,两条新闻越不相关
叉乘: 两个向量的叉积是另一个三维向量。叉积只对三维向量有意义。它有许多有用的属性,但最常用的一个是它与原来的两个向量都正交。 经常利用这个属性来求平面的法向量。
2.2 坐标系
什么是坐标系? 坐标系是建立图形与数之间对应联系的参考系
坐标系的分类
- 从维度上来看,分为一维、二维、三维等
- 从坐标轴之间的空间关系,可分为直角坐标系、极坐标系、圆柱坐标系、球坐标系等

在对一个事物进行建模(使用数学几何信息来描述物体)和观察(viewing)的过程中,并不总是使用同一个坐标系来考虑。图形显示的过程就是几何(对象)模型在不同坐标系之间的映射变换
计算机图形学中坐标系的分类
世界坐标系:世界坐标系是计算机图形学中用于定义整个虚拟世界空间的全局坐标系。它是所有物体和场景的共同参考框架,所有物体的位置、方向和大小等属性都是相对于世界坐标系来定义和计算的。

建模坐标系:又称为局部坐标系。每个物体(对象)有它自己的局部中心和坐标系

观察坐标系:观察坐标系是以观察者(如相机、视点等)为中心的坐标系。它定义了观察者的位置、观察方向以及观察区域的范围和形状,用于将世界坐标系中的物体转换到观察者视角下进行投影和显示。

设备坐标系:适合特定输出设备输出对象的坐标系。比如屏幕坐标系,在多数情况下,对于每一个具体的显示设备,都有一个单独的坐标系统- 定义图形在特定输出设备上的显示位置和大小,每个坐标对应设备上的一个像素。
- 与具体设备的分辨率相关,坐标范围由设备的分辨率决定。
- 在定义了显示窗口的情况下,可在设备坐标系中进一步定义称为视区的有限区域,视区中的成像即为实际所观察到的。
注意:设备坐标是整数
规范化坐标系:规范化坐标系是一种与设备无关的坐标系统,用于图形处理过程中,确保输出的图形在任何设备上都能保持一致。通常用于将观察坐标系中的坐标转换为设备坐标系之前的中间步骤。其坐标范围一般从-1到1或者0到1
2.3 二维图形变换
一个简单的图形,通过各种变换(如:比例、旋转、镜象 、错切、平移等)可以形成一个丰富多彩的图形或图案
在计算机动画中,经常有几个物体之间的相对运动,可以通过平移和旋转这些物体的局部坐标系得到这种动画效果
图形变换的基本原理
- 图形变化了,但原图形的
连边规则没有改变 - 图形的变化,是因为
顶点位置的改变决定的
变换图形就是要变换图形的几何关系,即改变顶点的坐标;同时,保持图形的原拓扑关系不变
仿射变换:是一种二维坐标到二维坐标之间的线性变换
- 平直性:直线经过变换之后依然是直线
- 平行性:平行线依然是平行线,且直线上 点的位置顺序不变)
2.4 齐次坐标
向量(x, y)经过变换后的点坐标为(x’, y’),这个变换过程可以写成如下矩阵形式

这种用三维向量表示二维向量,或者一般而言,用一个n+1维的向量表示一个n维向量的方法称为齐次坐标表示法


2.5 平移变换
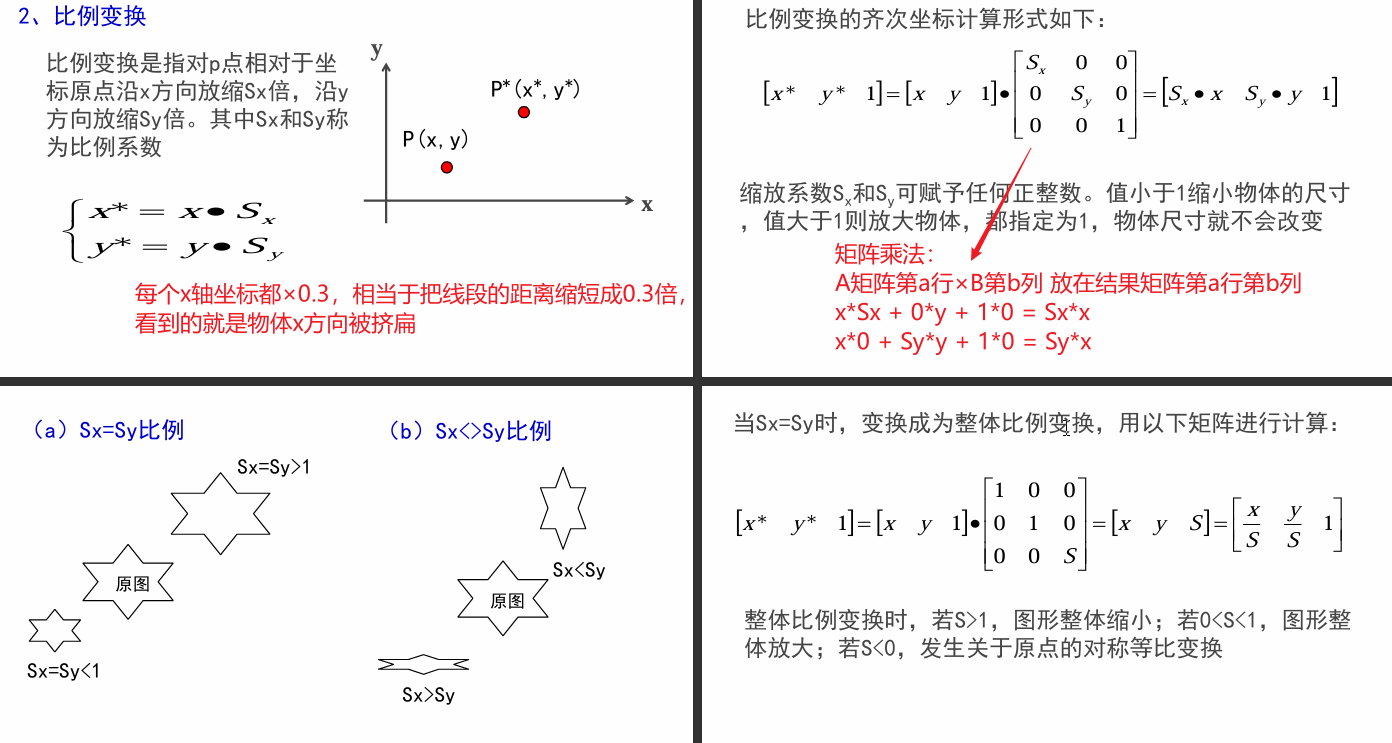
2.6 比例变换
2.7 对称变换
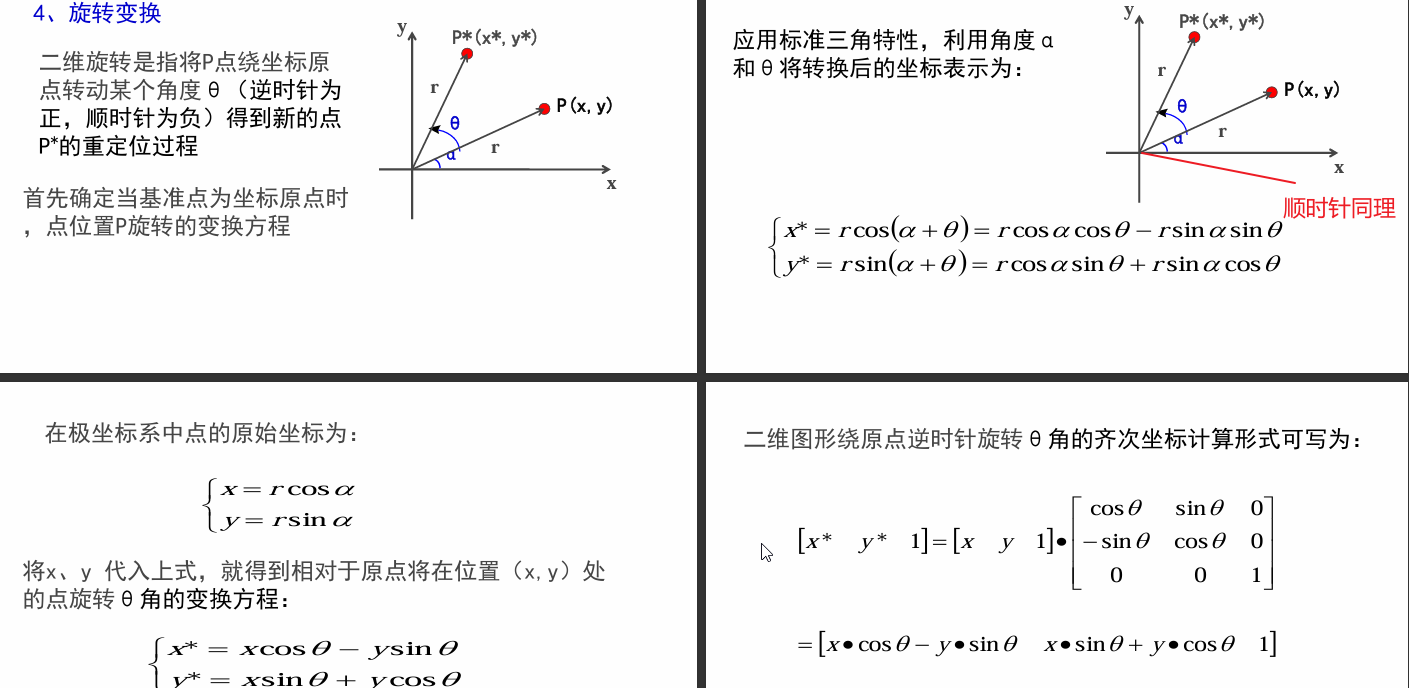
2.8 旋转变换
2.9 错切变换
2.10 复合变换
复合变换是指图形作一次以上的几何变换,变换结果是每次的变换矩阵相乘。从另一方面看,任何一个复杂的几何变换都可以看作基本几何变换的组合形式。
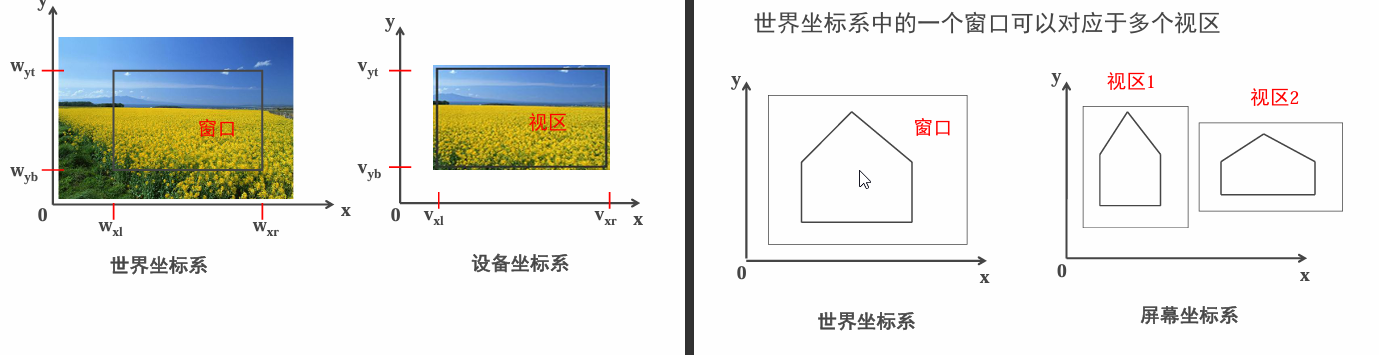
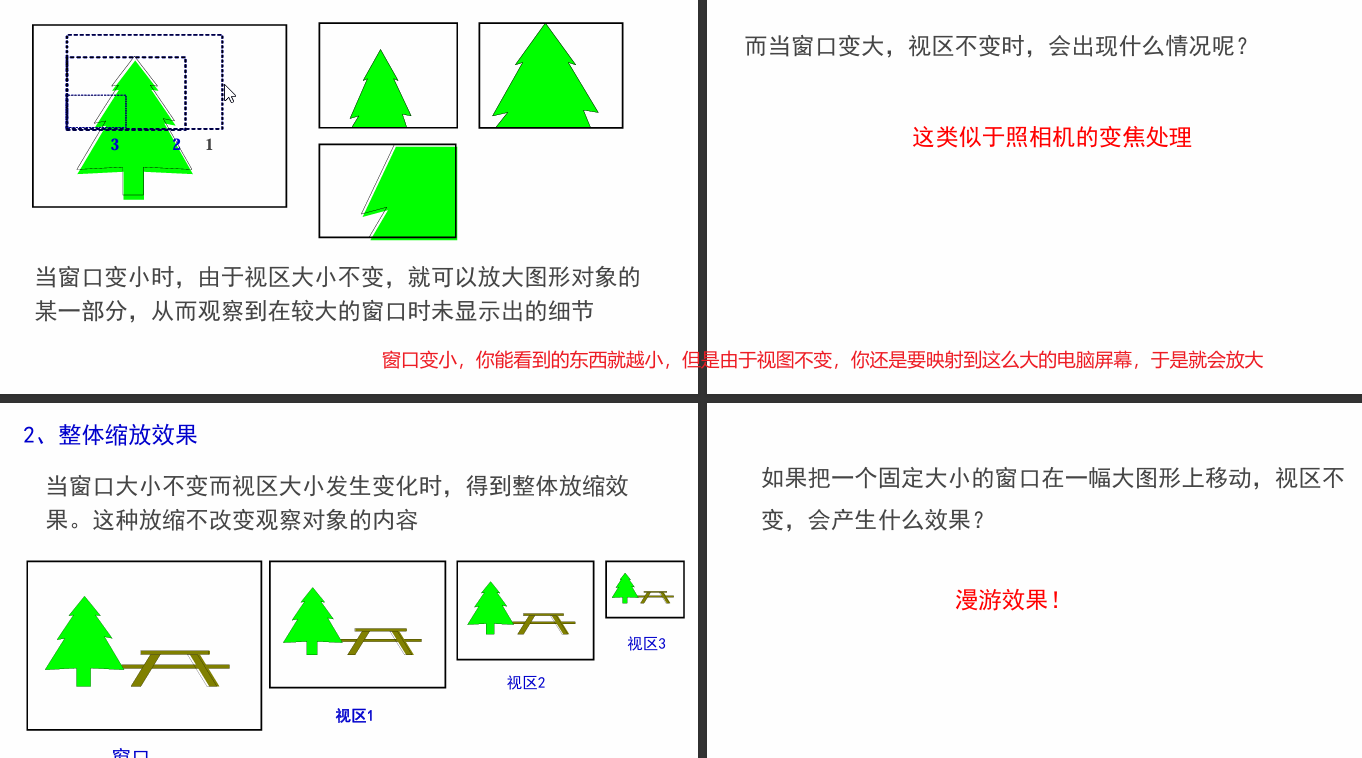
2.11 窗口、视区及变换
世界坐标系中要显示的区域(通常在观察坐标系内定义)称为窗口。窗口映射到显示器(设备)上的区域称为视区
窗口就是假定你的前方有一个能够透过光的玻璃,按物理学来说你能看到的区域。而视区就是将你能看到的事物映射到二维屏幕上。
如何将窗口内的图形在视区中显示出来呢? 必须经过将窗口到视区的变换处理,这种变换就是观察变换(Viewing Transformation)
2.12 最重要的
最重要的就是这个变换矩阵的每个元素会对二维图形造成什么影响
第三章 光栅图形学
光栅图形显示器可以看做一个像素的矩阵。在光栅显示器上显示的任何一种图形,实际上都是一些具有一种或多种颜色的像素集合。
首先介绍几个重要的概念:
图形的光栅化:确定最佳逼近图形的像素点集合,并使用指定属性写像素的过程
裁剪:任何图形进行光栅化时,必须显示在屏幕的一个窗口里,超出窗口的图形部分不予显示。确定一个图形的哪些部分在窗口内,必须显示;哪些部分落在窗口之外,不该显示的过程
走样和反走样:对图形进行光栅化时,由于显示器的空间分辨率有限,对于非水平垂直、±45°的直线,因像素逼近误差,使所画图形产生畸变(台阶、锯齿)的现象称之为走样(aliasing)。用于减少或消除走样的技术称为反走样(antialiasing)。
消隐:在真实感图形绘制过程中,由于投影变换失去了深度信息,会导致图形的二义性。消隐就是为了消除这类二义性,在绘制时消除被遮挡的不可见的线或面,以得到物体的真实图形。
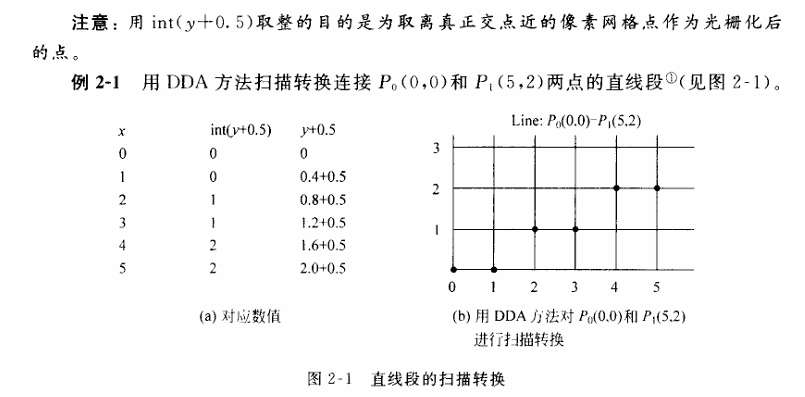
3.1 直线段的扫描转换算法
在数学上,理想的直线是没有宽度的,它是由无数个点构成的集合。对直线进行光栅化时,只能在显示器所给定的有限个像素组成的矩阵中,确定最佳逼近于该直线的一组像素,并且按扫描线顺序。
DDA数值微分算法
DDA算法基于直线的微分方程,DDA 算法基于直线的微分方程 $d y = k dx$ 和 $d x = \frac{1}{k} d y$,其中 $ k $ 是直线的斜率。通过选择最大位移方向作为步长方向,每次在该方向上移动一个单位长度,并根据斜率计算出另一个方向的增量,从而确定下一个像素点的位置。
- 确定直线方程和增量
- 根据给定的起点 $ P_0(x_0, y_0) $ 和终点 $ P_1(x_1, y_1) $,计算直线的斜率 $ k = \frac{y_1 - y_0}{x_1 - x_0} $。
- 选择在 $ x $ 或 $ y $ 方向作为步长方向,通常选择较大位移方向。若 $ |x_1 - x_0| > |y_1 - y_0| $,则以 $ x $ 方向为步长方向,否则以 $ y $ 方向为步长方向。
选择较大位移方向是为了提高精度
- 计算增量
- 若步长方向为 $ x $,则每次在 $ x $ 方向移动一个单位长度,即 $ \Delta x = 1 $,对应的 $ y $ 方向增量为 $ \Delta y = k $。
- 若步长方向为 $ y $,则每次在 $ y $ 方向移动一个单位长度,即 $ \Delta y = 1 $,对应的 $ x $ 方向增量为 $ \Delta x = \frac{1}{k} $。
- 逐点绘制
- 从起点开始,每次在步长方向移动一个单位长度,并根据计算的增量确定另一个方向的坐标,得到下一个像素点的坐标。
- 重复该过程,直到到达终点。
已知过端点 $P_0(x_0, y_0)$, $P_1(x_1, y_1)$ 的直线段 $L(P_0, P_1)$,直线斜率 $k = \frac{y_1 - y_0}{x_1 - x_0}$。画线过程为:从 $x$ 的左端点
$x_0$ 开始,向 $x$ 右端点步进,步长 = 1(像素),按 $y = kx + b$ 计算相应的 $y$ 坐标,并取像素点 $(x, \text{round}(y))$ 作为当前点的坐标。但
这样做,计算每一个点需要做一个乘法、一个加法。设步长为 $\Delta x$,有 $x_{i+1} = x_i + \Delta x$,于是:
$$y_{i+1} = kx_{i+1} + b = kx_i + k \Delta x + b = y_i + k \Delta x$$
当 $\Delta x = 1$ 时,则有 $y_{i+1} = y_i + k$;即 $x$ 每递增 1,$y$ 递增 $k$(即直线斜率)。这样,计算就由一个乘法和一个加法减少为一个加法。
在c++中,
int强转是截断小数点的,所以要加上0.5来确保四舍五入应当注意: 图中上述算法仅适用于
|k|<1的情形。在这种情况下,x每增加1,y最多增加1。当|k| > 1时,必须把x,y的地位互换,y每增加1,x相应增加1/k。在这个算法中,y与k必须用浮点数表示,而且每一步都要对y进行四舍五入后取整,这使得该算法不利于硬件实现。
- 优点
- 易于编程实现。
- 计算量较小,适合计算机图形学中的直线绘制。
- 缺点
- 绘制速度相对较慢,因为需要进行浮点运算。
- 精度有限,受设备精度的影响较大。
#include "widget.h"
#include "ui_widget.h"
#define cout qDebug()
Widget::Widget(QWidget *parent): QWidget(parent) , ui(new Ui::Widget)
{
ui->setupUi(this);
this->resize(800,400);
image = new QImage(rect().width(), rect().height(), QImage::Format_RGB32);
image->fill(Qt::white); // 初始化图像背景为白色
QPoint start(0, 0);
QPoint end(image->rect().width() - 1, image->rect().height() - 1);
// 使用DDA算法在Qimage上设置直线【像素点集合】
DDACalc(&start, &end, *image);update();
}
Widget::~Widget()
{
delete ui;
delete image; // 释放图像内存
}
void Widget::paintEvent(QPaintEvent *event) {
// 创建一个用于绘制到窗口的画家
QPainter painter(this);
// 绘制文字
painter.setRenderHint(QPainter::Antialiasing);
painter.setRenderHint(QPainter::NonCosmeticBrushPatterns); // 启用高抗锯齿
painter.setPen(Qt::blue);
painter.setFont(QFont("Arial", 16));
painter.drawText(QRect(0, 0, 200, 30), Qt::AlignCenter, "DDA算法画直线");
painter.drawImage(QRect(0, 0, image->rect().width(), image->rect().height()), *image);
// Qt自带的绘制直线函数
// QPoint start(0, 0);
// QPoint end(image->rect().width() - 1, image->rect().height() - 1);
// painter.drawLine(start, end);
}
// 此处只考虑了从左往右绘制的情况
void Widget::DDACalc(const QPoint *start, const QPoint *end, QImage &img) {
int dx = end->x() - start->x();
int dy = end->y() - start->y();
float k = dy / float(dx); // 求出斜率k
cout << "k = " <<k;
int steps = qMax(dx, dy);
qDebug() << steps;
if (steps == 0) { // 起点和终点重合
img.setPixel(start->x(), start->y(), qRgb(0, 0, 255));
return;
}
float x = start->x();
float y = start->y();
if(steps == dx){
for(int i = x; i <=steps; i++){
image->setPixel(i, int(y + 0.5), qRgb(0, 0, 255));
y = y + k;
}
}else{
for (int i = y; i<= steps; i++) {
image->setPixel(int(x + 0.5), i, qRgb(0, 0, 255));
x = x + 1.0 /k;
}
}
}中点画线法
https://zhuanlan.zhihu.com/p/468849410
算法核心思想:通过判断直线中点与理想直线的位置关系,决定下一像素点的选择。
- 参数预处理
- 输入起点
(x0, y0)和终点(x1, y1) - 计算坐标增量:
dx = x1 - x0
dy = y1 - y0 - 确定直线的主方向:
- 斜率绝对值 < 1:以
x为步进方向(水平主方向) - 斜率绝对值 ≥ 1:以
y为步进方向(垂直主方向)
- 斜率绝对值 < 1:以
- 决策变量公式推导
以 斜率 0 ≤ k ≤ 1 为例(其他斜率通过对称性处理):
- 直线隐式方程:
F(x, y) = dy·x - dx·y + dx·y0 - dy·x0 = 0 - 中点
M(x+1, y+0.5)到直线的距离由F(M)的符号决定:F(M) < 0→ 中点在直线下方 → 选择上方像素(x+1, y+1)F(M) ≥ 0→ 中点在上方或恰在直线上 → 选择下方像素(x+1, y)
- 决策变量初始值:
d = 2·dy - dx(简化后的整数形式)
- 递推公式
- 若
d < 0:
选择下方像素(x+1, y),更新决策变量:
d = d + 2·dy - 若
d ≥ 0:
选择上方像素(x+1, y+1),更新决策变量:
d = d + 2·(dy - dx)


void Widget::midpointLine(const QPoint& start, const QPoint& end, QImage& img) {
int x0 = start.x();
int y0 = start.y();
int x1 = end.x();
int y1 = end.y();
int dx = x1 - x0;
int dy = y1 - y0;
int d, x = x0, y = y0;
// 斜率小于1的情况
if (abs(dy) <= abs(dx)) {
d = dx - 2 * dy ;
while (x <= x1) {
img.setPixel(x, y, qRgb(0, 0, 0)); // 设置像素点颜色
if (d >= 0) {
d -= 2 * dy;
} else {
d += -2 * dy + 2 * dx;
y++;
}
x++;
}
}
// 斜率大于1的情况
else {
d = dy - 2 * dx;
while (y <= y1) {
img.setPixel(x, y, qRgb(0, 0, 0)); // 设置像素点颜色
if (d >= 0) {
d -= 2 * dx;
} else {
d += - 2 * dx + 2 * dy;
x++;
}
y++;
}
}
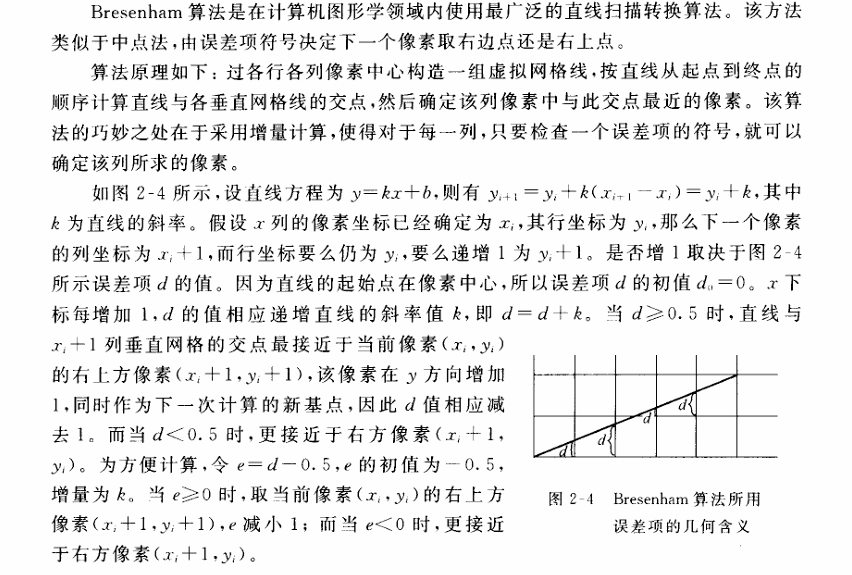
}Bresenham算法
void Widget::Bresenham(const QPoint& start, const QPoint& end, QImage& img) {
int x0 = start.x();
int y0 = start.y();
int x1 = end.x();
int y1 = end.y();
int dx = abs(x1 - x0);
int dy = abs(y1 - y0);
int sx = (x0 < x1) ? 1 : -1; // x方向步进(左/右)
int sy = (y0 < y1) ? 1 : -1; // y方向步进(上/下)
bool swapAxis = dy > dx; // 判断是否需要交换主轴
int error = swapAxis ? 2*dx - dy : 2*dy - dx; // 初始化误差项
int x = x0, y = y0;
// 根据主轴选择循环次数
int steps = swapAxis ? dy : dx;
for (int i = 0; i <= steps; i++) {
img.setPixel(x, y, qRgb(0, 0, 255));
if (swapAxis) {
// 以y轴为主方向
if (error >= 0) {
x += sx; // 副方向步进(x轴)
error -= 2*dy; // 修正误差项
}
error += 2*dx; // 主方向步进(y轴)
y += sy;
} else {
// 以x轴为主方向
if (error >= 0) {
y += sy; // 副方向步进(y轴)
error -= 2*dx; // 修正误差项
}
error += 2*dy; // 主方向步进(x轴)
x += sx;
}
}
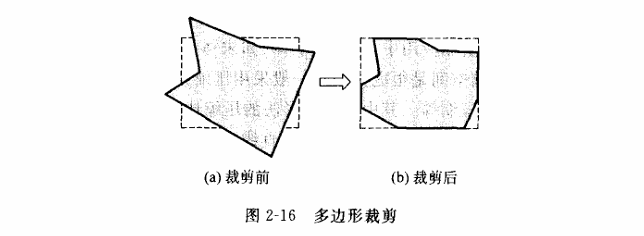
}3.2 多边形扫描算法
多边形分为凸多边形(任意两顶点间的连线均在多边形内)如图2-7(a)所示,凹多边形(任意两顶点间的连线可能有不在多边形内的部分)如图2-7(b)所示,含内环的多边形如图 2-7(c)所示

3.3 裁剪算法
使用计算机处理图形信息时,计算机内部存储的图形往往比较大,而屏幕显示的只是图的一部分,因此需要裁剪,提高显示效率。
3.2.1 直线段裁剪
Cohen-Sutherland 裁剪算法
该算法的思想是: 对于每条线段PP的处理分为3种情况。
若$P_1,P_2$完全在窗口内,则显示该线段,简称
取之若$P_1,P_2$:明显在窗口外,则丢弃该线段,简称
弃之。若线段既不满足“取”的条件,也不满足“弃”的条件,则在交点处把线段分为两段,其中一段完全在窗口外,可弃之;然后对另一段重复上述处理。


#include <iostream>
#include <vector>
using namespace std;
// 定义区域编码的位掩码
const int INSIDE = 0; // 0000
const int LEFT = 1; // 0001
const int RIGHT = 2; // 0010
const int BOTTOM = 4; // 0100
const int TOP = 8; // 1000
// 视口边界坐标
double x_min = 100, x_max = 400;
double y_min = 100, y_max = 300;
// 计算点的区域编码
int computeCode(double x, double y) {
int code = INSIDE;
if (x < x_min) code |= LEFT;
else if (x > x_max) code |= RIGHT;
if (y < y_min) code |= BOTTOM;
else if (y > y_max) code |= TOP;
return code;
}
// Cohen-Sutherland 裁剪算法
bool cohenSutherlandClip(double &x0, double &y0, double &x1, double &y1) {
int code0 = computeCode(x0, y0);
int code1 = computeCode(x1, y1);
bool accept = false;
while (true) {
if (!(code0 | code1)) { // 完全在视口内
accept = true;
break;
} else if (code0 & code1) { // 完全在视口外
break;
} else {
// 至少有一个点在外部,选择外部点进行裁剪
int codeOut = code0 ? code0 : code1;
double x, y;
// 计算与边界的交点
if (codeOut & TOP) { // 与上边界相交
x = x0 + (x1 - x0) * (y_max - y0) / (y1 - y0);
y = y_max;
} else if (codeOut & BOTTOM) { // 与下边界相交
x = x0 + (x1 - x0) * (y_min - y0) / (y1 - y0);
y = y_min;
} else if (codeOut & RIGHT) { // 与右边界相交
y = y0 + (y1 - y0) * (x_max - x0) / (x1 - x0);
x = x_max;
} else if (codeOut & LEFT) { // 与左边界相交
y = y0 + (y1 - y0) * (x_min - x0) / (x1 - x0);
x = x_min;
}
// 更新外部点为交点
if (codeOut == code0) {
x0 = x;
y0 = y;
code0 = computeCode(x0, y0);
} else {
x1 = x;
y1 = y;
code1 = computeCode(x1, y1);
}
}
}
return accept;
}
int main() {
// 示例线段:起点(50,150),终点(450,250)
double x0 = 50, y0 = 150;
double x1 = 450, y1 = 250;
if (cohenSutherlandClip(x0, y0, x1, y1)) {
cout << "裁剪后的线段端点:\n";
cout << "(" << x0 << ", " << y0 << ") -> ("
<< x1 << ", " << y1 << ")\n";
} else {
cout << "线段完全在视口外\n";
}
return 0;
}中点裁剪算法

梁友栋裁剪算法

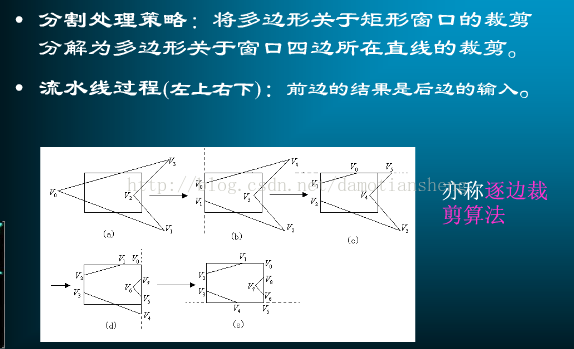
3.2.2 多边形裁剪 Suther land-Hodgeman算法
计算机图形学 学习笔记(五):多边形裁剪(Suther land-Hodgeman),文字裁剪_2sutherland的九区域代码的定义:-CSDN博客

基本策略是,先读取最开始的顶点V0和V3,对窗口左边做处理,得到交点L1和V3作为处理窗口下一条边的输入,然后对窗口上边做处理,输出L1和新的交点L2,然后这样不断读取下去,直到所有的点都处理过
第四章 真实感图形学
真实感图形学是计算机图形学中一个重要的组成部分,它的基本要求就是在计算机中生成二维场景的真实感图形图像,包括各类自然现象。
4.1 颜色视觉
从不同的角度来看,对于颜色有不同的要素或特性:
- 心理学和视觉角度:色调,饱和度和亮度
- 光学:主波长,纯度(对应于饱和度),明度(对应于亮度)
饱和度是指颜色的纯度,例如鲜红色的饱和度高,而粉红色的饱和度低。亮度就是光的强度,是光给人刺激的强度。
三色学说:任何一种颜色可以用红、绿、蓝三原色按照不同比例混合来得到
光学补充知识
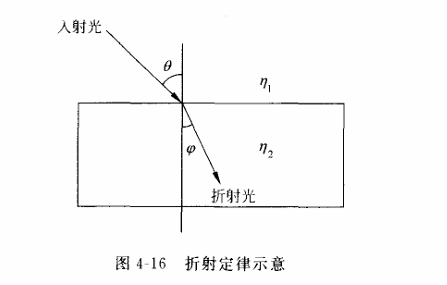
- 正常情况下,
光沿直线传播,当遇到不同的介质的分界面时,会产生反射和折射现象 - 反射定律:入射角等于反射角
折射定律:对应介质的折射率之比等于
入射线和折射线与法线构成的夹角的sin值之比
- 能量关系:能量是守恒的
光的度量:
- 立体角
- 点发光强度

4.2 简单光照模型
Pong光照模型
简单光照模型(Phong和Blinn-Phong)和明暗处理 - 芒果和小猫 - 博客园
Blinn-Phong光照模型与着色方法 - Tim’s Note
基本组成



相关向量
- 法线向量(Normal Vector):垂直于表面的向量,用于表示表面的方向。
- 视图向量(View Vector):指向观察者方向的向量。
- 光线向量(Light Vector):指向光源方向的向量。
- 反射向量(Reflection Vector):表示光线在表面反射后的方向。
特点
- 简单高效:Phong模型相对简单,计算成本较低,能够快速地为物体表面提供较为真实的光照效果。
- 可调节性强:通过调整各个反射系数和高光指数等参数,可以模拟不同材质的光照效果。
在Phong光照模型中,确定某个点的RGB值需要综合考虑环境光、漫反射光和镜面反射光这三种光照分量。以下是具体的计算过程:
1. 环境光(Ambient Light)
环境光是模拟场景中普遍存在的光,与物体表面的朝向无关。其计算公式为:
$ I_a = k_a \cdot I_{a_{\text{source}}} $
其中:
- $ I_a $ 是环境光对物体表面的贡献。
- $ k_a $ 是物体表面对环境光的反射系数,通常是一个 RGB 向量。
- $ I_{a_{\text{source}}} $ 是环境光的强度,也是一个 RGB 向量。
例如,假设环境光的强度为 $ I_{a_{\text{source}}} = (0.2, 0.2, 0.2) $,物体表面对环境光的反射系数为 $ k_a = 0.1 $,则环境光的贡献为:
$ I_a = 0.1 \cdot (0.2, 0.2, 0.2) = (0.02, 0.02, 0.02) $2. 漫反射光(Diffuse Light)
漫反射光是光线照射到物体表面后,向各个方向均匀反射的光。其计算公式为:
$ I_d = k_d \cdot I_{d_{\text{source}}} \cdot \max(0, \vec{N} \cdot \vec{L}) $
其中:
- $ I_d $ 是漫反射光对物体表面的贡献。
- $ k_d $ 是物体表面对漫反射光的反射系数,通常是一个 RGB 向量。
- $ I_{d_{\text{source}}} $ 是光源的漫反射强度,也是一个 RGB 向量。
- $ \vec{N} $ 是物体表面的法线向量,需要归一化。
- $ \vec{L} $ 是从物体表面点指向光源的方向向量,也需要归一化。
- $ \vec{N} \cdot \vec{L} $ 是法线向量和光线方向向量的点积,表示光线与表面的夹角。
例如,假设光源的漫反射强度为 $ I_{d_{\text{source}}} = (1.0, 1.0, 1.0) $,物体表面对漫反射光的反射系数为 $ k_d = 0.5 $,法线向量为 $ \vec{N} = (0, 1, 0) $,光线方向向量为 $ \vec{L} = (0, 1, 0) $,则漫反射光的贡献为:
$ \vec{N} \cdot \vec{L} = 1 $
$ I_d = 0.5 \cdot (1.0, 1.0, 1.0) \cdot 1 = (0.5, 0.5, 0.5) $3. 镜面反射光(Specular Light)
镜面反射光是光线照射到光滑表面后,按照反射定律反射的部分。其计算公式为:
$ I_s = k_s \cdot I_{s_{\text{source}}} \cdot \max(0, \vec{R} \cdot \vec{V})^n $
其中:
- $ I_s $ 是镜面反射光对物体表面的贡献。
- $ k_s $ 是物体表面对镜面反射光的反射系数,通常是一个 RGB 向量。
- $ I_{s_{\text{source}}} $ 是光源的镜面反射强度,也是一个 RGB 向量。
- $ \vec{R} $ 是反射光线方向向量,可以通过公式 $ \vec{R} = 2(\vec{N} \cdot \vec{L})\vec{N} - \vec{L} $ 计算得到。
- $ \vec{V} $ 是从物体表面点指向观察者的方向向量,需要归一化。
- $ n $ 是高光指数,用于控制高光的锐度,数值越大,高光越集中。
例如,假设光源的镜面反射强度为 $ I_{s_{\text{source}}} = (1.0, 1.0, 1.0) $,物体表面对镜面反射光的反射系数为 $ k_s = 0.5 $,高光指数为 $ n = 32 $,反射光线方向向量为 $ \vec{R} = (0, 1, 0) $,观察者方向向量为 $ \vec{V} = (0, 1, 0) $,则镜面反射光的贡献为:
$ \vec{R} \cdot \vec{V} = 1 $
$ I_s = 0.5 \cdot (1.0, 1.0, 1.0) \cdot 1^{32} = (0.5, 0.5, 0.5) $4. 最终颜色计算
将上述三种光照分量相加,得到物体表面某一点的最终颜色:
$ I = I_a + I_d + I_s $假设物体的颜色为 $ \text{objectColor} = (1.0, 0.5, 0.3) $,则最终颜色为:
$ I = (0.02, 0.02, 0.02) + (0.5, 0.5, 0.5) + (0.5, 0.5, 0.5) $
$ I = (1.02, 1.02, 1.02) $由于 RGB 值的范围是 [0, 1],因此需要将最终颜色值限制在 [0, 1] 范围内:
$ I = \text{clamp}(I, 0, 1) = (1.0, 1.0, 1.0) $最终,该点的 RGB 值为 $ (1.0, 1.0, 1.0) $,表示该点在 Phong 光照模型下的颜色为白色。
示例代码(基于 OpenGL 的片段着色器)
以下是一个简单的 OpenGL 片段着色器代码,用于计算 Phong 光照模型下的颜色:
>// 片段着色器 >#version 330 core >out vec4 FragColor; >in vec3 FragPos; // 片段位置 >in vec3 Normal; // 片段法线 >uniform vec3 lightPos; // 光源位置 >uniform vec3 viewPos; // 观察者位置 >uniform vec3 lightColor; // 光源颜色 >uniform vec3 objectColor; // 物体颜色 >void main() >{ // 环境光 float ka = 0.1; vec3 ambient = ka * lightColor; // 漫反射 float kd = 1.0; vec3 N = normalize(Normal); vec3 L = normalize(lightPos - FragPos); float NdotL = max(dot(N, L), 0.0); vec3 diffuse = kd * NdotL * lightColor; // 镜面反射 float ks = 0.5; float shininess = 32.0; vec3 V = normalize(viewPos - FragPos); vec3 R = reflect(-L, N); float spec = pow(max(dot(V, R), 0.0), shininess); vec3 specular = ks * spec * lightColor; // 最终颜色 vec3 result = (ambient + diffuse + specular) * objectColor; FragColor = vec4(result, 1.0); >}
4.3 增量式光照模型
Phong光照明模型中光源和视点都被假定为无穷远,最后的光强计算公式就变为物体表面法向量的函数。这样对于当前流行的显示系统中用多边形表示的物体来说,它们中的每一个多边形由于法向一致,因而多边形内部像素的颜色都是相同的。
因此在不同法向的多边形邻接处,不仅有光强突变,而且还会产生马赫带效应_百度百科,即人类视觉系统夸大具有不同常量光强的两个相邻区域之间的光强不连续性。
为了保证多边形之间的光滑过渡,使连续的多边形呈现匀称的光强分布,可采用下面将要介绍的增量式光照明模型。模型的基本思想是:在每一个多边形的顶点处,计算合适的光照明强度或其他参数;然后在各个多边形内部进行均匀插值;最后得到多边形的光滑颜色分布。它包含两种主要形式:
双线性光强插值和双线性法向插值,又被分别称为Gouraud明暗处理和Phong明暗处理。
双线性光强插值

双线性法向插值
4.4 局部光照模型
4.5 透射模型
4.6 光线追踪算法
【计算机图形学】深入浅出讲解光线追踪(Ray Tracing)_cg 光线追踪-CSDN博客
第五章 几何造型技术
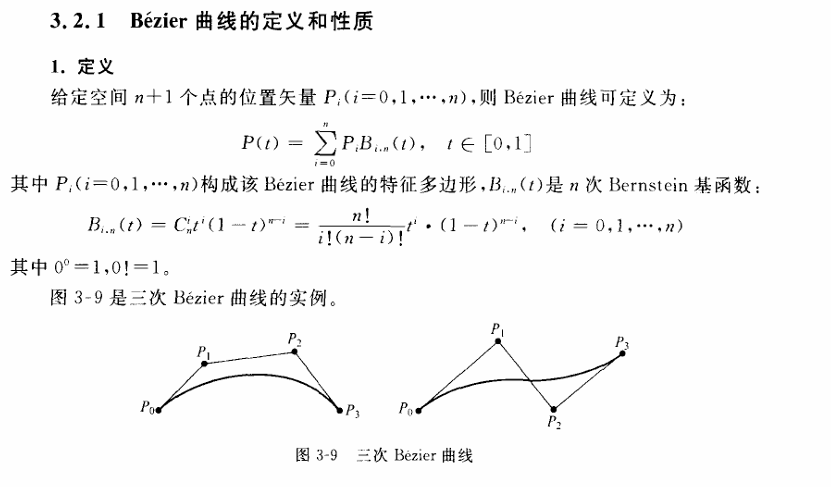
5.1 贝塞尔曲线曲面
设 $P0,P1$ 是平面的任意两点,则 $P0,P1$ 两点连线的参数方程可表示为:
$B1(t)=(1−t)P0+tP1$
其中,$t$为参数,$t∈[0,1]$,当$t$等于0时,该点就是$P0$,当t为1时,该点为$P1$
曲线上任意一点 $P(t)$ 的坐标可以通过以下公式得到:
$P(t)=(1 - t)P_0+tP_1$
展开到二维坐标,$P(t)$ 的 x 坐标和 y 坐标分别为:
$\begin{cases} x(t)=(1 - t)x_0+tx_1\ y(t)=(1 - t)y_0+ty_1 \end{cases}$
这里的 $(1 - t)$ 和 t 就是一次贝塞尔基本函数,分别记为 $B_{0,1}(t)=1 - t$ 和 $B_{1,1}(t)=t$。
贝塞尔曲线实现代码:
from math import factorial # 这是阶乘函数
import matplotlib.pyplot as plt
points = [[0,0],[1,3],[4,3],[6,0],[7,2.5],[10,6]]# 在此处修改坐标,控制点
N = len(points)
n = N - 1 # 控制点数量-1就是几次贝塞尔曲线
px = []
py = []
for T in range(1001):
t = T*0.001
x,y = 0,0
for i in range(N):
# 贝塞尔曲线推导公式
B = factorial(n)*t**i*(1-t)**(n-i)/(factorial(i)*factorial(n-i))
x += points[i][0]*B
y += points[i][1]*B
px.append(x)
py.append(y)
plt.plot(px,py)
plt.plot([i[0] for i in points],[i[1] for i in points],'r.')
plt.show()贝塞尔曲面
from math import factorial
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 控制点(二维数组,每个元素是一个控制点的三维坐标)
points = [
[[0, 0, 0], [1, 3, 1], [4, 3, 2], [6, 0, 3]],
[[1, 1, 1], [2, 4, 2], [5, 4, 3], [7, 1, 4]],
[[2, 2, 2], [3, 5, 3], [6, 5, 4], [8, 2, 5]],
[[3, 3, 3], [4, 6, 4], [7, 6, 5], [9, 3, 6]]
]
# 获取控制点的行数和列数
rows = len(points)
cols = len(points[0])
# 计算阶数
n = rows - 1
m = cols - 1
# 存储曲面上的点
px = []
py = []
pz = []
# 遍历曲面上的每个点
for U in range(101):
u = U * 0.01
for V in range(101):
v = V * 0.01
x, y, z = 0, 0, 0
# 计算贝塞尔曲面公式
for i in range(rows):
for j in range(cols):
B1 = factorial(n) * u ** i * (1 - u) ** (n - i) / (factorial(i) * factorial(n - i))
B2 = factorial(m) * v ** j * (1 - v) ** (m - j) / (factorial(j) * factorial(m - j))
x += points[i][j][0] * B1 * B2
y += points[i][j][1] * B1 * B2
z += points[i][j][2] * B1 * B2
px.append(x)
py.append(y)
pz.append(z)
# 创建3D图形
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# 绘制贝塞尔曲面
ax.scatter(px, py, pz, s=1)
# 绘制控制点
control_px = [point[0] for row in points for point in row]
control_py = [point[1] for row in points for point in row]
control_pz = [point[2] for row in points for point in row]
ax.scatter(control_px, control_py, control_pz, c='r', marker='o')
# 显示图形
plt.show()5.2 B样条曲线曲面

B样条(BSpline,即 Basis Spline) - MarsCactus - 博客园
大作业
https://www.doubao.com/thread/w4ea59255743f4494
Phong模型
Phong模型认为物体的反射光照主要由三个部分构成
环境光:物体背对光源的部分,但是仍然会有光线经过其他物体的反射间接地照射到物体表面,然后被人眼接收镜面反射:或者叫高光,一般是由物体的光滑表面完全不发散的反射到人眼中漫反射:是投射在粗糙表面上的光向各个方向反射相对平均亮度的光照到人眼
从上到下依次是镜面反射,漫反射和环境光
代码实现
Vector3向量类实现 - 在代码中即用来代表光强(rgb)又用来代表空间的3维向量
向量点积和叉积的定义是不同的,请参考以下博客向量点乘与叉乘的概念及几何意义 - 知乎
class Vector3
{
public:
double x, y, z;
Vector3() : x(0), y(0), z(0) {}//构造函数,防垃圾值
Vector3(double newX, double newY,double newZ)
{
x = newX;
y = newY;
z = newZ;
}
//向量加法
Vector3 operator+(const Vector3 &a)const
{
return Vector3(x + a.x, y + a.y, z + a.z);
}
//向量减法
Vector3 operator-(const Vector3& a)const
{
return Vector3(x - a.x, y - a.y, z - a.z);
}
//向量数乘
Vector3 operator*(double a)const
{
return Vector3(x * a, y * a, z * a);
}
//向量数除
Vector3 operator/(double a)const
{
return Vector3(x / a, y / a, z / a);
}
//向量点积
double operator*(const Vector3& a)const
{
return ((x * a.x)+(y * a.y)+(z * a.z)); // https://baike.baidu.com/item/点积/9648528 点积的值可以知道两个向量角度关系
}
//向量模长
static double getlen(const Vector3& a)
{
return sqrt(a * a);
}
//向量单位化
static Vector3 unitization(const Vector3& a)
{
return a / getlen(a);
}
};// normal表示法向量
Vector3 calculatePhongLighting(const Vector3& hitPoint, const Vector3& normal, const Light& light, const Vector3& camera, const Sphere& sphere)
{
Vector3 mixcol;
mixcol.x=light.color.x * sphere.color.x;
mixcol.y=light.color.y * sphere.color.y;
mixcol.z=light.color.z * sphere.color.z;
Vector3 ambient = mixcol * 0.15; // 环境光(0.15是环境光系数)
// 漫反射
Vector3 lightDir = Vector3::unitization(light.position - hitPoint); // 这是打击点指向光源的方向向量
double diff = std::max(normal * lightDir, 0.0);// 漫反射系数,法向量和方向向量的点积 -> 数字越大表示两个向量越像,反射的光强越大 至于为什么--https://zhuanlan.zhihu.com/p/670938197
Vector3 diffuse = mixcol * diff;
// 镜面反射
Vector3 viewDir = Vector3::unitization(camera - hitPoint);
Vector3 reflectDir = Vector3::unitization(normal * 2.0 * (normal * lightDir) - lightDir);
double spec = std::pow(std::max(viewDir * reflectDir, 0.0), 32);//32是镜面高光指数 spec是镜面发射因子
Vector3 specular = light.color * 0.5 * spec; //0.5镜面反射系数 (颜色)
// 合并颜色并限制范围
Vector3 result = ambient + diffuse + specular;
result.x = std::clamp(result.x, 0.0, 1.0);
result.y = std::clamp(result.y, 0.0, 1.0);
result.z = std::clamp(result.z, 0.0, 1.0);
// 映射到 0-255
return result * 255.0;
}我在这里有一个小疑问:为什么在计算漫反射的时候反射系数是用
打击点指向光源的方向向量计算,而到了镜面反射之后就是用打击点指向相机的向量和反射向量计算了?https://www.doubao.com/thread/w72544395a6157aed
- 漫反射的物理现象
漫反射发生在粗糙表面(如纸张、墙壁),光线入射后会向各个方向均匀散射。此时,观察者从任意角度看到的漫反射亮度仅取决于光源的入射角度,与观察位置无关。例如:无论从哪个方向看一张白纸,其亮度不会有明显变化,因为光线被均匀散射到了所有方向。
- 数学模型中的向量选择
根据 Lambert 定律,漫反射强度与表面法线向量 $\vec{N}$ 和光源方向向量 $\vec{L}$ 的夹角余弦值成正比($\vec{L}$ 通常定义为从表面点指向光源的单位向量)。公式表示为:$\text{漫反射项} = k_d \cdot (\vec{N} \cdot \vec{L})$ 这里只需要光源方向 $\vec{L}$,因为漫反射的 “均匀性” 决定了它不依赖观察方向。即使观察者移动,表面接收到的光源入射角度不变,漫反射强度也不会改变。
- 镜面反射的物理现象
镜面反射发生在光滑表面(如镜子、金属),光线会按照反射定律(入射角等于反射角)定向反射。此时,只有当反射光恰好指向观察者时,才能看到明亮的高光(Specular Highlight)。例如:观察镜子时,只有特定角度才能看到光源的反射像,偏离角度后高光消失。

光线追踪
点击链接查看和Kimi的对话 https://www.kimi.com/share/d13dskivtfeo7d4217j0
Snell定律
入射角和折射角与法线夹角的正弦sin值之比 等于 折射率之比 https://www.doubao.com/thread/wa4b654f88a820cd0

// 计算折射向量(Snell定律)
/*
* I : 入射光线的单位向量(从折射点指向光源)
* N : 法向量的单位向量
* eta_ratio : eta_ratio:折射率比值(入射介质折射率 / 折射介质折射率,例如从空气到水为 1.0/1.33)
*/
static Vector3 refract(const Vector3& I, const Vector3& N, double eta_ratio) {
double cosi = std::clamp(I * N, -1.0, 1.0); // 点积表示向量余弦值, clamp函数限制余弦值范围
Vector3 n = N;
if (cosi < 0) { // 入射向量和法向量不是同一方向的
cosi = -cosi;
} else {
n = n * -1.0; // 调整法线方向
eta_ratio = 1.0 / eta_ratio; // 调整折射率为倒数
}
double k = 1.0 - eta_ratio * eta_ratio * (1.0 - cosi * cosi);
// 全反射情况处理
return k < 0 ? Vector3(0, 0, 0) : (I * eta_ratio + n * (eta_ratio * cosi - std::sqrt(k)));
}光线类的定义
计算机图形学知识点——光线追踪(Ray Tracing) - 知乎
//Ray类的建立 A+t*B
class Ray
{
public:
Vector3 A=camera; // 光线的起点
Vector3 B; // 光线方向向量
float t; // 代表光线上的一点,任意一点可以通过 A + B * t 计算得到。
Ray() : A(), B(), t(0) {}//构造函数,防垃圾值
Ray(Vector3 newA, Vector3 newB, float newt) : A(newA), B(newB), t(newt) {
A = newA;
B = newB;
B = Vector3::unitization(B);
t = newt;
}
// Vector3 ProjectivePoint(float t)const//得到射影点
// {
// return A + B * t;
// }
};判断光线和物体碰撞

static bool if_Hit(Vector3 center, double radius, Ray ray)
{
double a = ray.B * ray.B;
double b = 2.0 * (ray.B * (ray.A-center));
double c = (ray.A-center) *(ray.A-center) - radius * radius;
double delta = b * b - 4 * a * c; // 判别式用于判断二次方程是否有实根。如果 delta≥0,则方程有实根,表明光线与球体相交
// 使用求根公式计算两个根 x1 和 x2,代表光线与球体相交的两个参数值
float x1=(-b+sqrt(delta))/(2*a);
float x2=(-b-sqrt(delta))/(2*a);
// 选择较小的根 t(因为光线是从起点向外延伸的,较小的根表示更近的交点)。
// 如果较小的根 t≤0,则检查较大的根是否大于 0,如果是,则使用较大的根。表示至少有一个交点是在视线中的
float t=(x1<x2?x1:x2);
if(t<=0&&(x1>x2?x1:x2)>0)
{
t=(x1>x2?x1:x2);
}
return (delta >= 0)&&(t>0);
}光线追踪的阴影处理
// ===== 场景管理类 =====
class Scene {
public:
std::vector<Object*> objects; // 场景中的物体列表
std::vector<Light> lights; // 场景中的光源列表
Vector3 backgroundColor; // 背景颜色
int maxDepth; // 光线追踪最大递归深度
Scene() : backgroundColor(0.1, 0.2, 0.3), maxDepth(5) {}
~Scene() {
// 释放所有物体内存
for (auto obj : objects)
delete obj;
}
void addObject(Object* obj) { objects.push_back(obj); }
void addLight(const Light& light) { lights.push_back(light); }
// 检测光线与场景中物体的相交 intersect 函数返回最近交点的距离 t 和物体指针 hitObject,是光线追踪的基础函数
bool intersect(const Ray& ray, double& t, Object*& hitObject) const {
t = std::numeric_limits<double>::max(); // 初始化为无穷大
hitObject = nullptr;
// 遍历所有物体,寻找最近的交点
for (auto obj : objects) {
double currentT = t;
if (obj->intersect(ray, currentT) && currentT < t) {
t = currentT;
hitObject = obj;
}
}
return hitObject != nullptr;
}
// 阴影检测:判断点是否在光源的阴影中
/*
*
* 判断阴影条件
* 点光源:若射线与物体相交,比较交点距离 t 与光源距离 lightDist。若 t < lightDist,说明物体在光源之前,point 于阴影中
* 方向光:方向光被视为无限远,只要射线与任何物体相交,即认为 point 处于阴影中
*
*/
bool isInShadow(const Vector3& point, const Light& light) const {
Vector3 lightDir;
if (light.type == POINT_LIGHT) {
lightDir = Vector3::unitization(light.position - point); // 点光源方向
} else {
lightDir = Vector3::unitization(light.position * -1.0); // 方向光方向
}
// 偏移起点避免浮点误差导致的自相交
Ray shadowRay(point + lightDir * 0.001, lightDir, 0);
double t;
Object* hitObject;
// 射线检测:调用 intersect 函数检测射线是否与场景中的物体相交。若不相交,直接返回 false(无阴影)
if (intersect(shadowRay, t, hitObject)) {
// 点光源需要判断交点是否在光源之前
if (light.type == POINT_LIGHT) {
double lightDist = Vector3::getlen(light.position - point);
return t < lightDist;
}
return true; // 方向光只要相交即处于阴影
}
return false;
}
};抗锯齿采样
#include <QApplication>
#include <QImage>
#include <QLabel>
#include <QPixmap>
#include <QPainter>
#include <QColor>
#include <cmath>
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//向量类的创建(运算法则)
class Vector3
{
public:
double x, y, z;
Vector3() : x(0), y(0), z(0) {}//构造函数,防垃圾值
Vector3(double newX, double newY,double newZ)
{
x = newX;
y = newY;
z = newZ;
}
//向量加法
Vector3 operator+(const Vector3 &a)const
{
return Vector3(x + a.x, y + a.y, z + a.z);
}
//向量减法
Vector3 operator-(const Vector3& a)const
{
return Vector3(x - a.x, y - a.y, z - a.z);
}
//向量数乘
Vector3 operator*(double a)const
{
return Vector3(x * a, y * a, z * a);
}
//向量数除
Vector3 operator/(double a)const
{
return Vector3(x / a, y / a, z / a);
}
//向量点积
double operator*(const Vector3& a)const
{
return ((x * a.x)+(y * a.y)+(z * a.z)); // https://baike.baidu.com/item/点积/9648528 点积的值可以知道两个向量角度关系
}
//向量模长
static double getlen(const Vector3& a)
{
return sqrt(a * a);
}
//向量单位化
static Vector3 unitization(const Vector3& a)
{
return a / getlen(a);
}
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//光屏平面的位置
static double z=500.0;
//摄像机位置(A)
static Vector3 camera(0.0,0.0,0.0);
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//Sphere类的创建
class Sphere // 球类
{
public:
Vector3 center;
double radius;
Vector3 color; // 球体颜色
Sphere() : center(), radius(0.0), color(0, 0, 0) {} // 构造函数,防垃圾值
Sphere(Vector3 newCenter, double newRadius, Vector3 newColor) :
center(newCenter), radius(newRadius), color(newColor) {} // 赋值构造函数
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//light(光源)类的建立
struct Light {
Vector3 position; // 光源位置
Vector3 color; // 光源颜色(通常为 RGB 值)
double intensity; // 光源强度(可选,用于控制光照强度)
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//引入冯氏光照模型 phong(返回计算出的物体表面光照效果颜色)
// normal 法向量
Vector3 calculatePhongLighting(const Vector3& hitPoint, const Vector3& normal, const Light& light, const Vector3& camera, const Sphere& sphere)
{
Vector3 mixcol;
mixcol.x=light.color.x * sphere.color.x;
mixcol.y=light.color.y * sphere.color.y;
mixcol.z=light.color.z * sphere.color.z;
Vector3 ambient = mixcol * 0.15; // 环境光(0.15是环境光系数)
// 漫反射
Vector3 lightDir = Vector3::unitization(light.position - hitPoint); // 这是打击点 指向光源的方向向量
double diff = std::max(normal * lightDir, 0.0);//漫反射系数,点积的数值越大,两个向量越像,漫反射光强越大
Vector3 diffuse = mixcol * diff;
// 镜面反射
Vector3 viewDir = Vector3::unitization(camera - hitPoint); // 打击点指向相机
Vector3 reflectDir = Vector3::unitization(normal * 2.0 * (normal * lightDir) - lightDir);
double spec = std::pow(std::max(viewDir * reflectDir, 0.0), 32);//32是镜面高光指数 spec是镜面发射因子
Vector3 specular = light.color * 0.5 * spec; //0.5镜面反射系数 (颜色)
// 合并颜色并限制范围
Vector3 result = ambient + diffuse + specular;
result.x = std::clamp(result.x, 0.0, 1.0);
result.y = std::clamp(result.y, 0.0, 1.0);
result.z = std::clamp(result.z, 0.0, 1.0);
// 映射到 0-255
return result * 255.0;
}
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//Ray类的建立 A+t*B
class Ray
{
public:
Vector3 A=camera; // 光线的起点
Vector3 B; // 光线方向向量
float t; // 代表光线上的一点,任意一点可以通过 A + B * t 计算得到。
Ray() : A(), B(), t(0) {}//构造函数,防垃圾值
Ray(Vector3 newA, Vector3 newB, float newt) : A(newA), B(newB), t(newt) {
A = newA;
B = newB;
B = Vector3::unitization(B);
t = newt;
}
Vector3 ProjectivePoint(float t)const//得到射影点
{
return A + B * t;
}
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// 平面地面的光照计算
Vector3 calculateGroundLighting(double y, const Light &light)
{
Vector3 groundColor(100.0 / 255.0, 100.0 / 255.0, 100.0 / 255.0); // 地面颜色
Vector3 normal(0, 1, 0); // 地面法线始终向上
Vector3 mixcol;
mixcol.x = light.color.x * groundColor.x;
mixcol.y = light.color.y * groundColor.y;
mixcol.z = light.color.z * groundColor.z;
Vector3 ambient = mixcol * 0.15; // 环境光
// 漫反射
Vector3 lightDir = Vector3::unitization(light.position - Vector3(0, y, z));
double diff = std::max(normal * lightDir, 0.0);
Vector3 diffuse = mixcol * diff;
// 地面没有镜面反射
Vector3 result = ambient + diffuse;
result.x = std::clamp(result.x, 0.0, 1.0);
result.y = std::clamp(result.y, 0.0, 1.0);
result.z = std::clamp(result.z, 0.0, 1.0);
return result * 255.0;
}
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//光线撞击相关函数
//是否撞击的判断
// center:球体的中心位置。 radius:球体的半径。 ray:表示光线,包含起点(A)、方向向量(B)和参数(t)。
static bool if_Hit(Vector3 center, double radius, Ray ray)
{
double a = ray.B * ray.B;
double b = 2.0 * (ray.B * (ray.A-center));
double c = (ray.A-center) *(ray.A-center) - radius * radius;
double delta = b * b - 4 * a * c; // 判别式用于判断二次方程是否有实根。如果 delta≥0,则方程有实根,表明光线与球体相交
// 使用求根公式计算两个根 x1 和 x2,代表光线与球体相交的两个参数值
float x1=(-b+sqrt(delta))/(2*a);
float x2=(-b-sqrt(delta))/(2*a);
// 选择较小的根 t(因为光线是从起点向外延伸的,较小的根表示更近的交点)。
// 如果较小的根 t≤0,则检查较大的根是否大于 0,如果是,则使用较大的根。表示至少有一个交点是在视线中的
float t=(x1<x2?x1:x2);
if(t<=0&&(x1>x2?x1:x2)>0)
{
t=(x1>x2?x1:x2);
}
return (delta >= 0)&&(t>0); // 假如t<0表示交点在视线射线的(人)背后方向,delta是二元一次方程求根公式
}
//求解撞击法向量,并线性变换得到rgb编码(但是我就不判断撞不撞击了,使用时需要在前面加一个if(bool if_Hit)判断)
static Vector3 where_Hit(Vector3 center, double radius, Ray ray)
{
ray.B=Vector3:: unitization(ray.B);
float a = ray.B * ray.B;
float b = 2.0 * (ray.B * (ray.A-center));
float c = (ray.A-center) *(ray.A- center) - radius * radius;
float delta = b * b - 4 * a * c;
float x1=(-b+sqrt(delta))/(2*a);
float x2=(-b-sqrt(delta))/(2*a);
float t=(x1<x2?x1:x2);
if(t<=0&&(x1>x2?x1:x2)>0)
{
t=(x1>x2?x1:x2);
}
if(t>=0)
{
Vector3 Lawline=ray.A+ray.B*t-center;
//引入phong应该不需要rgb转化了,这是之前为了便于验证的代码
// Lawline=Vector3::unitization(Lawline);//单位化
// Lawline = (Lawline + Vector3(1, 1, 1)) / 2;
// Lawline = Lawline * 255;//向0~255作线性映射(为了颜色好看,改了一下,可能以后变数据会出问题,注意一下)
return Lawline;
}
else
{
Vector3 black=Vector3(0,0,0);
return black;
// Vector3 Lawline=ray.A+ray.B*t-center;
// Lawline=Vector3::unitization(Lawline);//单位化
// Vector3 Unit(1,1,1);
// Lawline=(Lawline+Unit)/2*255;//向0~255作线性映射(为了颜色好看,改了一下,可能以后变数据会出问题,注意一下)
// return Lawline;
}
}
//多重取样 抗锯齿(采用phong后)【对于地面球】
/*
使用双重循环进行 2x2 采样:newx 和 newy:计算当前采样点在视口中的坐标。
创建光线 ray,起点为相机位置,方向向量指向采样点。
判断光线与球体相交
调用 if_Hit 判断光线是否与球体相交:
如果相交:
计算相交点 hitPoint。
计算法线向量 normal。
调用 calculatePhongLighting 计算光照效果,并存储颜色。
如果不相交:
使用背景颜色填充采样颜色。
处理采样结果
如果所有采样点都未命中球体,返回特殊值 (-1, -1, -1)。
否则:
计算所有采样颜色的平均值。
将颜色值限制在 [0.0, 255.0] 范围内。
返回平均颜色。
*/
Vector3 multisample(double x, double y, const Sphere& sphere, const Light& light) {
const int sample = 2; // 采样数量
Vector3 sample_color[sample * sample];
int n = 0;
int count=0;
for (int i = 0; i < sample; i++)
{
for (int j = 0; j < sample; j++)
{
float newx = x - 0.5 + (i + 0.5) / sample;
float newy = y - 0.5 + (j + 0.5) / sample;
Ray ray(camera, Vector3(newx, newy, z), 0);
if (if_Hit(sphere.center, sphere.radius, ray))
{
Vector3 hitPoint = where_Hit(sphere.center, sphere.radius, ray);
Vector3 normal = Vector3::unitization(hitPoint - sphere.center);
sample_color[n++] = calculatePhongLighting(hitPoint, normal, light, camera, sphere);
}
else
{
count++;
sample_color[n++] = Vector3(135 + 120 * y / 301, 206 + 50 * y / 301, 255); // 背景颜色
}
}
}
if(count==sample*sample)
{
return Vector3(-1,-1,-1);
}
else
{
Vector3 average_color = sample_color[0];
for (int i = 1; i < sample * sample; i++) {
average_color = average_color + sample_color[i];
}
average_color = average_color / (sample * sample);
// 平均颜色后(ai生成的限制范围的方式)
average_color.x = std::clamp(average_color.x, 0.0, 255.0);
average_color.y = std::clamp(average_color.y, 0.0, 255.0);
average_color.z = std::clamp(average_color.z, 0.0, 255.0);
return average_color;
}
/*
static Vector3 multisample(double x,double y,Sphere R)
{
const int sample=2;
Vector3 sample_point[sample*sample];
int n=0;
for(int i=0;i<sample;i++)
{
for(int j=0;j<sample;j++)
{
// float newx=x-0.5+i;
// float newy=y-0.5+j;
float newx = x - 0.5 + (i + 0.5) / sample;
float newy = y - 0.5 + (j + 0.5) / sample;
// float newx=x-0.5+4/sample/sample*i;
// float newy=y-0.5+4/sample/sample*j;
Ray Hit_R(camera, Vector3(newx, newy, z),0);//0是随意赋的值,无实义
bool flag=if_Hit(R.center,R.radius,Hit_R);
if(flag)
{
sample_point[n]=where_Hit(R.center,R.radius,Hit_R);
n++;
}
else
{
double px=(x-camera.x+800/2);
double py=(y-camera.y+600/2);
sample_point[n]=Vector3(135+120*py/601,206+50*py/601,255);
n++;
}//对2*2个样本点实现了采集
}
}//对2*2个样本点实现了采集
Vector3 average=sample_point[0];
for(int i=1;i<sample*sample;i++)
{
average=average+sample_point[i];
}
average=average/sample/sample;
//ai搜到的,防止越界的函数
average.x = std::clamp((float)average.x, 0.0f, 255.0f);
average.y = std::clamp((float)average.y, 0.0f, 255.0f);
average.z = std::clamp((float)average.z, 0.0f, 255.0f);
return average;
}
*/
}
//多重取样 抗锯齿(采用phong后)【对于地上球】
/*
* x 和 y:当前像素的坐标。
*
*
*/
Vector3 multisample2(double x, double y, const Sphere& sphere, const Light& light,const Sphere& groundsphere) {
const int sample = 2; // 采样数量
Vector3 sample_color[sample * sample];
int n = 0;
int count1=0;
int count2=0;
for (int i = 0; i < sample; i++)
{
for (int j = 0; j < sample; j++)
{
float newx = x - 0.5 + (i + 0.5) / sample;
float newy = y - 0.5 + (j + 0.5) / sample;
Ray ray(camera, Vector3(newx, newy, z), 0); // 整个画面是 右x 上y 向屏幕里面z
if (if_Hit(sphere.center, sphere.radius, ray))
{
Vector3 hitPoint = where_Hit(sphere.center, sphere.radius, ray);
Vector3 normal = Vector3::unitization(hitPoint - sphere.center);
sample_color[n++] = calculatePhongLighting(hitPoint, normal, light, camera, sphere);
}
else
{
if(if_Hit(groundsphere.center, groundsphere.radius, ray))
{
count1++;
Vector3 hitPoint = where_Hit(groundsphere.center, groundsphere.radius, ray);
Vector3 normal = Vector3::unitization(hitPoint - groundsphere.center);
sample_color[n++] = calculatePhongLighting(hitPoint, normal, light, camera, groundsphere);
}
else
{
count2++;
sample_color[n++] = Vector3(135 + 120 * y / 301, 206 + 50 * y / 301, 255); // 背景颜色
}
}
}
}
if(count1==sample*sample||count2==sample*sample)
{
return Vector3(-1,-1,-1);
}
else
{
Vector3 average_color = sample_color[0];
for (int i = 1; i < sample * sample; i++) {
average_color = average_color + sample_color[i];
}
average_color = average_color / (sample * sample);
// 平均颜色后(ai生成的限制范围的方式)
average_color.x = std::clamp(average_color.x, 0.0, 255.0);
average_color.y = std::clamp(average_color.y, 0.0, 255.0);
average_color.z = std::clamp(average_color.z, 0.0, 255.0);
return average_color;
}
}
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//窗口,输出一张图片
class ImageWidget : public QWidget
{
protected:
void paintEvent(QPaintEvent *event) override
{
QPainter painter(this);
// 创建一个 401x301 的 QImage,并初始化为白色
QImage image(401, 301, QImage::Format_RGB32);//修改图片大小的时候记得回到multisample更改一下
image.fill(Qt::white); // 可选:设置初始背景颜色
// 将每个像素点设置为渐变青
for (int y = 0; y <image.height() ; ++y)
{
for (int x =0 ; x <image.width() ; ++x)
{
QColor color(135+120*y/image.height(),206+50*y/image.height(),255); // 渐变青
image.setPixel(x, y, color.rgb());
}
}
Light light;
light.position = Vector3(0,-300, 600);
light.color = Vector3(255.0 / 255.0, 255.0 / 255.0, 100.0 / 255.0); // 暖色调光源
light.intensity=500.0;
// 建立地面球R0(
Sphere R0(Vector3(0, 1800, z), 1800.0, Vector3(100.0/255.0, 100.0/255.0, 100.0/255.0));
for (int y = 0; y < image.height(); ++y)
{
for (int x = 0; x < image.width(); ++x)
{
// 世界坐标系转化
double true_x = (double)camera.x - (double)(image.width() - 1)/2.0 + (double)x;
double true_y = (double)camera.y - (double)(image.height() - 1)/2.0 + (double)y;
Vector3 color0 = multisample(true_x, true_y, R0, light);
if(color0.x != -1 && color0.y != -1 && color0.z != -1)
{
image.setPixel(x, y, QColor(color0.x, color0.y, color0.z).rgb());
}
}
}
// // 地面颜色计算
// for (int y =image.height()*3/5; y <image.height() ; ++y)
// {
// Vector3 groundColor = calculateGroundLighting(y, light);
// for (int x = 0; x < image.width(); ++x)
// {
// image.setPixel(x, y, QColor(groundColor.x, groundColor.y, groundColor.z).rgb());
// }
// }
//建立球R1
Sphere R1(Vector3(0, 0, z), 50.0, Vector3(0.0/255.0, 255.0/255.0, 0.0/255.0)); // 绿色球
for (int y = 0; y <image.height() ; y++)
{
for (int x =0 ; x <image.width() ; x++)
{
//世界坐标系转化
double true_x=(double)camera.x-(double)(image.width() - 1)/2.0f+(double)x;
double true_y=(double)camera.y-(double)(image.height() - 1)/2.0f+(double)y;
// Ray Hit_R1(camera,Vector3(true_x,true_y,z),0);//0是随意赋的值,无实义
// bool flag=if_Hit(R1.center,R1.radius,Hit_R1);
// if(flag)
// {
// Vector3 point=multisample(true_x,true_y,R1);
// QColor color2(point.x,point.y,point.z);
Vector3 color = multisample2(true_x, true_y, R1, light,R0);
if(color.x!=-1&&color.y!=-1&&color.z!=-1)
{
image.setPixel(x, y, QColor(color.x, color.y, color.z).rgb());//渲染球体
}
}
}
// 绘制图像到窗口
painter.drawImage(0, 0, image);
}
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
int main(int argc, char *argv[])
{
QApplication app(argc, argv);
ImageWidget widget;
widget.resize(401, 301);// 设置窗口大小
widget.show();
return app.exec();
}新版代码
#include <QApplication>
#include <QImage>
#include <QLabel>
#include <QPixmap>
#include <QPainter>
#include <QColor>
#include <cmath>
#include <vector>
#include <QMouseEvent>
#include <QKeyEvent>
#include <QTimer>
#include <random>
// ===== 数学基础:三维向量类 =====
class Vector3 {
public:
double x, y, z; // 三维向量的三个分量
Vector3() : x(0), y(0), z(0) {}
Vector3(double newX, double newY, double newZ) : x(newX), y(newY), z(newZ) {}
// 向量基本运算重载
Vector3 operator+(const Vector3& a) const { return Vector3(x + a.x, y + a.y, z + a.z); } // 向量加法
Vector3 operator-(const Vector3& a) const { return Vector3(x - a.x, y - a.y, z - a.z); } // 向量减法
Vector3 operator*(double a) const { return Vector3(x * a, y * a, z * a); } // 向量与标量乘法
Vector3 operator/(double a) const { return Vector3(x / a, y / a, z / a); } // 向量与标量除法
double operator*(const Vector3& a) const { return x * a.x + y * a.y + z * a.z; } // 向量点积(返回标量)
// 逐元素相乘(Hadamard乘积),用于颜色混合
Vector3 hadamard(const Vector3& a) const {
return Vector3(x * a.x, y * a.y, z * a.z);
}
// 向量叉积,用于计算法向量和相机坐标系
Vector3 cross(const Vector3& a) const {
return Vector3(y * a.z - z * a.y, z * a.x - x * a.z, x * a.y - y * a.x);
}
// 向量工具函数
static double getlen(const Vector3& a) { return std::sqrt(a * a); } // 计算向量长度
static Vector3 unitization(const Vector3& a) { return a / getlen(a); } // 向量归一化
static Vector3 reflect(const Vector3& I, const Vector3& N) { // 计算反射向量
return I - N * 2.0 * (I * N); // I表示入射光线,N表示法向量
}
// 计算折射向量(Snell定律)
/*
* I : 入射光线的单位向量(从折射点指向光源)
* N : 法向量的单位向量
* eta_ratio : eta_ratio:折射率比值(入射介质折射率 / 折射介质折射率,例如从空气到水为 1.0/1.33)
*/
static Vector3 refract(const Vector3& I, const Vector3& N, double eta_ratio) {
double cosi = std::clamp(I * N, -1.0, 1.0); // 点积表示向量余弦值, clamp函数限制余弦值范围
Vector3 n = N;
if (cosi < 0) { // 入射向量和法向量不是同一方向的
cosi = -cosi;
} else {
n = n * -1.0; // 调整法线方向
eta_ratio = 1.0 / eta_ratio; // 调整折射率为倒数
}
double k = 1.0 - eta_ratio * eta_ratio * (1.0 - cosi * cosi);
// 全反射情况处理
return k < 0 ? Vector3(0, 0, 0) : (I * eta_ratio + n * (eta_ratio * cosi - std::sqrt(k)));
}
};
// ===== 场景元素定义 =====
// 光源类型枚举
enum LightType {
POINT_LIGHT, // 点光源(从一点向四周发射光线)
DIRECTIONAL_LIGHT // 方向光(平行光,如太阳光)
};
// 光源结构体
struct Light {
LightType type; // 光源类型
Vector3 position; // 点光源位置 / 方向光方向向量
Vector3 color; // 光源颜色
double intensity; // 光源强度
};
// 材质属性结构体(定义物体表面光学特性)
struct Material {
Vector3 ambient; // 环境光反射系数
Vector3 diffuse; // 漫反射系数
Vector3 specular; // 镜面反射系数
double shininess; // 光泽度(控制高光范围) 控制镜面反射高光的大小和锐利程度。值越大,高光越集中、越亮;值越小,高光越分散、越模糊。
double reflectivity; // 反射率 控制物体表面反射周围环境的能力,即镜面反射光线的比例。
double transparency; // 透明度
double refractiveIndex; // 折射率
};
// ===== 光线定义 =====
class Ray {
public:
Vector3 A; // 光线起点
Vector3 B; // 光线方向(已归一化)
float t; // 光线参数
Ray() : A(), B(), t(0) {}
Ray(Vector3 newA, Vector3 newB, float newt) : A(newA), B(Vector3::unitization(newB)), t(newt) {}
// 计算光线上参数t处的点
Vector3 ProjectivePoint(float t) const { return A + B * t; }
};
// ===== 场景物体基类 =====
class Object {
public:
Material material; // 物体材质
Object() = default;
virtual ~Object() = default;
// 纯虚函数:检测光线与物体是否相交
virtual bool intersect(const class Ray& ray, double& t) const = 0;
// 纯虚函数:获取物体表面法向量
virtual Vector3 getNormal(const Vector3& point) const = 0;
};
// ===== 球体类(继承自物体基类)=====
class Sphere : public Object {
public:
Vector3 center; // 球心位置
double radius; // 球体半径
Sphere(Vector3 newCenter, double newRadius, Material mat) : center(newCenter), radius(newRadius) {
material = mat;
}
// 光线与球体相交检测(使用二次方程求解),判断是否相交就是求Δ判别式
bool intersect(const Ray& ray, double& t) const override {
Vector3 oc = ray.A - center; // 光线起点到球心的向量
double a = ray.B * ray.B; // 二次项系数
double b = 2.0 * (oc * ray.B); // 一次项系数
double c = oc * oc - radius * radius; // 常数项
double discriminant = b * b - 4 * a * c; // 判别式
if (discriminant < 0) return false; // 无实根,不相交
double sqrtDisc = std::sqrt(discriminant);
double t1 = (-b - sqrtDisc) / (2.0 * a); // 第一个交点
double t2 = (-b + sqrtDisc) / (2.0 * a); // 第二个交点
// 选择最近的有效交点(t>0)
if (t1 > 0 && t1 < t) {
t = t1;
return true;
}
if (t2 > 0 && t2 < t) {
t = t2;
return true;
}
return false;
}
// 获取球体表面法向量(指向球外)
Vector3 getNormal(const Vector3& point) const override {
return Vector3::unitization(point - center);
}
};
// ===== 平面类(继承自物体基类)=====
class Plane : public Object {
public:
Vector3 normal; // 平面法线
double d; // 平面方程参数 (ax + by + cz + d = 0)
Plane(Vector3 normal, double d, Material mat) : normal(Vector3::unitization(normal)), d(d) {
material = mat;
}
// 光线与平面相交检测
bool intersect(const Ray& ray, double& t) const override {
double denom = normal * ray.B; // 光线方向与法线的点积
if (std::abs(denom) < 1e-6) return false; // 光线与平面平行
double t0 = -(normal * ray.A + d) / denom; // 求解交点参数
if (t0 > 0 && t0 < t) { // 只接受t>0的有效交点
t = t0;
return true;
}
return false;
}
// 获取平面法向量(始终为定义的法线)
Vector3 getNormal(const Vector3&) const override {
return normal;
}
};
// ===== 场景管理类 =====
class Scene {
public:
std::vector<Object*> objects; // 场景中的物体列表
std::vector<Light> lights; // 场景中的光源列表
Vector3 backgroundColor; // 背景颜色
int maxDepth; // 光线追踪最大递归深度
Scene() : backgroundColor(0.1, 0.2, 0.3), maxDepth(5) {}
~Scene() {
// 释放所有物体内存
for (auto obj : objects)
delete obj;
}
void addObject(Object* obj) { objects.push_back(obj); }
void addLight(const Light& light) { lights.push_back(light); }
// 检测光线与场景中物体的相交 intersect 函数返回最近交点的距离 t 和物体指针 hitObject,是光线追踪的基础函数
bool intersect(const Ray& ray, double& t, Object*& hitObject) const {
t = std::numeric_limits<double>::max(); // 初始化为无穷大
hitObject = nullptr;
// 遍历所有物体,寻找最近的交点
for (auto obj : objects) {
double currentT = t;
if (obj->intersect(ray, currentT) && currentT < t) {
t = currentT;
hitObject = obj;
}
}
return hitObject != nullptr;
}
// 阴影检测:判断点是否在光源的阴影中
/*
*
* 判断阴影条件
* 点光源:若射线与物体相交,比较交点距离 t 与光源距离 lightDist。若 t < lightDist,说明物体在光源之前,point 于阴影中
* 方向光:方向光被视为无限远,只要射线与任何物体相交,即认为 point 处于阴影中
*
*/
bool isInShadow(const Vector3& point, const Light& light) const {
Vector3 lightDir;
if (light.type == POINT_LIGHT) {
lightDir = Vector3::unitization(light.position - point); // 点光源方向
} else {
lightDir = Vector3::unitization(light.position * -1.0); // 方向光方向
}
// 偏移起点避免浮点误差导致的自相交
Ray shadowRay(point + lightDir * 0.001, lightDir, 0);
double t;
Object* hitObject;
// 射线检测:调用 intersect 函数检测射线是否与场景中的物体相交。若不相交,直接返回 false(无阴影)
if (intersect(shadowRay, t, hitObject)) {
// 点光源需要判断交点是否在光源之前
if (light.type == POINT_LIGHT) {
double lightDist = Vector3::getlen(light.position - point);
return t < lightDist;
}
return true; // 方向光只要相交即处于阴影
}
return false;
}
};
// ===== UI窗口类(继承自QWidget)=====
class ImageWidget : public QWidget {
Q_OBJECT
private:
Vector3 cameraPos; // 相机位置
Vector3 cameraTarget; // 相机目标点
Vector3 upVector; // 相机上方向向量
double cameraSpeed; // 相机移动速度
double rotationSpeed; // 相机旋转速度
Scene scene; // 渲染场景
QImage image; // 渲染图像
bool isRendering; // 渲染状态标记
int samplesPerPixel; // 每像素采样数(抗锯齿)
std::mt19937 rng; // 随机数生成器(用于采样)
public:
ImageWidget() :
cameraPos(0, 0, -5), // 初始相机位置
cameraTarget(0, 0, 0), // 初始观察点
upVector(0, 1, 0), // 初始上方向
cameraSpeed(0.2), // 相机移动速度
rotationSpeed(0.01), // 相机旋转速度
isRendering(false), // 初始未渲染
samplesPerPixel(1) // 初始采样数
{
resize(800, 600); // 设置窗口大小
image = QImage(width(), height(), QImage::Format_RGB32); // 创建渲染图像
// 初始化随机数生成器
std::random_device rd;
rng = std::mt19937(rd());
// 设置场景(添加物体和光源)
setupScene();
// 延迟启动渲染
QTimer::singleShot(100, this, &ImageWidget::render);
}
// 场景设置函数
void setupScene() {
// 定义不同材质(红色漫反射、蓝色漫反射、金属、玻璃、地面)
Material redDiffuse = {
Vector3(0.1, 0.0, 0.0), // 环境光
Vector3(0.8, 0.1, 0.1), // 漫反射
Vector3(1.0, 1.0, 1.0), // 镜面反射
32.0, // 光泽度
0.2, // 反射率
0.0, // 透明度
1.0 // 折射率
};
Material blueDiffuse = {
Vector3(0.0, 0.0, 0.1),
Vector3(0.1, 0.1, 0.8),
Vector3(1.0, 1.0, 1.0),
32.0,
0.2,
0.0,
1.0
};
Material reflective = {
Vector3(0.1, 0.1, 0.1),
Vector3(0.3, 0.3, 0.3),
Vector3(0.8, 0.8, 0.8),
128.0,
0.8,
0.0,
1.0
};
Material glass = {
Vector3(0.0, 0.0, 0.0),
Vector3(0.0, 0.0, 0.0),
Vector3(1.0, 1.0, 1.0),
64.0,
0.2,
0.9,
1.5
};
Material floorMat = {
Vector3(0.1, 0.1, 0.1),
Vector3(0.7, 0.7, 0.7),
Vector3(0.5, 0.5, 0.5),
32.0,
0.3,
0.0,
1.0
};
// 添加球体到场景
scene.addObject(new Sphere(Vector3(-1.0, 0.0, 0.0), 0.5, redDiffuse));
scene.addObject(new Sphere(Vector3(1.0, 0.0, 0.0), 0.5, blueDiffuse));
scene.addObject(new Sphere(Vector3(0.0, 0.0, 1.0), 0.5, reflective));
scene.addObject(new Sphere(Vector3(0.0, -0.5, -0.5), 0.5, glass));
// 添加地面平面
scene.addObject(new Plane(Vector3(0, 1, 0), 1.0, floorMat));
// 添加光源(点光源和方向光)
Light light1;
light1.type = POINT_LIGHT;
light1.position = Vector3(3, 5, -2);
light1.color = Vector3(1, 1, 1);
light1.intensity = 1.0;
scene.addLight(light1);
Light light2;
light2.type = DIRECTIONAL_LIGHT;
light2.position = Vector3(-1, -1, -1);
light2.color = Vector3(0.8, 0.8, 0.9);
light2.intensity = 0.5;
scene.addLight(light2);
}
// 光线追踪核心函数:递归计算光线与场景的交互
Vector3 traceRay(const Ray& ray, int depth) const {
if (depth > scene.maxDepth) return scene.backgroundColor; // 达到最大递归深度,返回背景色
double t;
Object* hitObject = nullptr;
if (!scene.intersect(ray, t, hitObject)) return scene.backgroundColor; // 无相交,返回背景色
Vector3 hitPoint = ray.ProjectivePoint(t); // 计算交点
Vector3 normal = hitObject->getNormal(hitPoint); // 获取交点法向量
Vector3 viewDir = Vector3::unitization(cameraPos - hitPoint); // 视图方向
// 环境光分量(直接使用材质环境光系数)
Vector3 ambient = hitObject->material.ambient;
// 漫反射和镜面反射分量(逐光源计算)
Vector3 diffuse(0, 0, 0);
Vector3 specular(0, 0, 0);
for (const auto& light : scene.lights) {
if (scene.isInShadow(hitPoint, light)) continue; // 点在阴影中,跳过
Vector3 lightDir;
if (light.type == POINT_LIGHT) {
lightDir = Vector3::unitization(light.position - hitPoint); // 点光源方向
} else {
lightDir = Vector3::unitization(light.position * -1.0); // 方向光方向
}
// 漫反射计算:Phong模型
double diff = std::max(normal * lightDir, 0.0); // 漫反射强度(余弦值裁剪为非负)
double scalarFactor = diff * light.intensity; // 标量因子(强度×余弦值)
// 物体漫反射颜色 × 光源颜色(逐元素相乘)× 标量因子
diffuse = diffuse + hitObject->material.diffuse.hadamard(light.color) * scalarFactor;
// 镜面反射计算:Phong模型
Vector3 reflectDir = Vector3::reflect(lightDir * -1.0, normal); // 反射方向
double spec = std::pow(std::max(viewDir * reflectDir, 0.0), hitObject->material.shininess); // 镜面反射强度
// 物体镜面反射颜色 × 光源颜色 × 标量因子
specular = specular + hitObject->material.specular.hadamard(light.color) * spec * light.intensity;
}
// 反射分量(递归追踪反射光线)
Vector3 reflection(0, 0, 0);
if (hitObject->material.reflectivity > 0) {
Vector3 reflectDir = Vector3::reflect(ray.B * -1.0, normal); // 反射方向
// 偏移起点避免自相交
Ray reflectRay(hitPoint + reflectDir * 0.001, reflectDir, 0);
reflection = traceRay(reflectRay, depth + 1) * hitObject->material.reflectivity; // 递归追踪
}
// 折射分量(递归追踪折射光线)
Vector3 refraction(0, 0, 0);
if (hitObject->material.transparency > 0) {
bool inside = normal * ray.B > 0; // 判断光线是进入还是离开物体
Vector3 refractedNormal = inside ? normal * -1.0 : normal; // 调整折射法线方向
double eta = inside ? hitObject->material.refractiveIndex : 1.0 / hitObject->material.refractiveIndex; // 折射率
Vector3 refractDir = Vector3::refract(ray.B, refractedNormal, eta); // 计算折射方向
if (refractDir.x != 0 || refractDir.y != 0 || refractDir.z != 0) { // 非零折射方向
Ray refractRay(hitPoint + refractDir * 0.001, refractDir, 0); // 偏移起点
refraction = traceRay(refractRay, depth + 1) * hitObject->material.transparency; // 递归追踪
}
}
// 合并所有光照分量
Vector3 color = ambient + diffuse + specular + reflection + refraction;
// 颜色值范围裁剪(0.0-1.0)
color.x = std::clamp(color.x, 0.0, 1.0);
color.y = std::clamp(color.y, 0.0, 1.0);
color.z = std::clamp(color.z, 0.0, 1.0);
return color;
}
// 图像渲染函数
void render() {
if (isRendering) return; // 避免重复渲染
isRendering = true;
image.fill(Qt::black); // 清空图像
// 构建相机坐标系(视图空间)
Vector3 viewDir = Vector3::unitization(cameraTarget - cameraPos); // 视图方向
Vector3 right = Vector3::unitization(viewDir.cross(upVector)); // 右方向
Vector3 up = right.cross(viewDir); // 上方向
// 相机参数设置
double fov = 60.0 * M_PI / 180.0; // 视场角(弧度)
double aspectRatio = static_cast<double>(width()) / height(); // 宽高比
double halfHeight = std::tan(fov / 2.0); // 半高
double halfWidth = aspectRatio * halfHeight; // 半宽
// 随机数分布(用于抗锯齿采样)
std::uniform_real_distribution<double> dist(0.0, 1.0);
// 逐像素渲染(外循环:行,内循环:列)
for (int y = 0; y < height(); ++y) {
for (int x = 0; x < width(); ++x) {
Vector3 pixelColor(0, 0, 0);
// 多重采样抗锯齿:每个像素采样多个点取平均
for (int s = 0; s < samplesPerPixel; ++s) {
// 在像素内添加随机偏移(抖动采样)
double u = (x + dist(rng)) / (width() - 1);
double v = (height() - 1 - y + dist(rng)) / (height() - 1);
// 构建视平面坐标系
Vector3 lowerLeftCorner = cameraPos + viewDir - right * halfWidth - up * halfHeight;
Vector3 horizontal = right * 2.0 * halfWidth;
Vector3 vertical = up * 2.0 * halfHeight;
// 计算光线方向
Vector3 direction = lowerLeftCorner + horizontal * u + vertical * v - cameraPos;
Ray ray(cameraPos, direction, 0);
// 追踪光线并累加颜色
pixelColor = pixelColor + traceRay(ray, 0);
}
// 平均采样颜色
pixelColor = pixelColor / samplesPerPixel;
// 伽马校正(补偿显示器非线性响应)
pixelColor.x = std::sqrt(pixelColor.x);
pixelColor.y = std::sqrt(pixelColor.y);
pixelColor.z = std::sqrt(pixelColor.z);
// 转换为QColor并设置像素
int r = static_cast<int>(255.99 * pixelColor.x);
int g = static_cast<int>(255.99 * pixelColor.y);
int b = static_cast<int>(255.99 * pixelColor.z);
image.setPixel(x, y, qRgb(r, g, b));
}
// 每渲染10行更新一次显示,提供进度反馈
if (y % 10 == 0)
update();
}
isRendering = false;
update(); // 渲染完成后更新显示
}
protected:
// 绘图事件处理
void paintEvent(QPaintEvent* event) override {
QPainter painter(this);
painter.drawImage(0, 0, image); // 绘制渲染图像
if (isRendering) {
painter.setPen(Qt::white);
painter.drawText(10, 20, "Rendering..."); // 显示渲染状态
}
}
// 键盘事件处理(相机控制)
void keyPressEvent(QKeyEvent* event) override {
bool needUpdate = false;
// 相机移动控制
switch (event->key()) {
case Qt::Key_W: // 向前移动
cameraPos = cameraPos + Vector3::unitization(cameraTarget - cameraPos) * cameraSpeed;
needUpdate = true;
break;
case Qt::Key_S: // 向后移动
cameraPos = cameraPos - Vector3::unitization(cameraTarget - cameraPos) * cameraSpeed;
needUpdate = true;
break;
case Qt::Key_A: // 向左移动
cameraPos = cameraPos - Vector3::unitization(Vector3::unitization(cameraTarget - cameraPos).cross(upVector)) * cameraSpeed;
needUpdate = true;
break;
case Qt::Key_D: // 向右移动
cameraPos = cameraPos + Vector3::unitization(Vector3::unitization(cameraTarget - cameraPos).cross(upVector)) * cameraSpeed;
needUpdate = true;
break;
case Qt::Key_Up: // 向上移动观察点
cameraTarget = cameraTarget + upVector * cameraSpeed;
needUpdate = true;
break;
case Qt::Key_Down: // 向下移动观察点
cameraTarget = cameraTarget - upVector * cameraSpeed;
needUpdate = true;
break;
case Qt::Key_Left: // 向左移动观察点
cameraTarget = cameraTarget - Vector3::unitization(Vector3::unitization(cameraTarget - cameraPos).cross(upVector)) * cameraSpeed;
needUpdate = true;
break;
case Qt::Key_Right: // 向右移动观察点
cameraTarget = cameraTarget + Vector3::unitization(Vector3::unitization(cameraTarget - cameraPos).cross(upVector)) * cameraSpeed;
needUpdate = true;
break;
case Qt::Key_Space: // 重置相机
cameraPos = Vector3(0, 0, -5);
cameraTarget = Vector3(0, 0, 0);
needUpdate = true;
break;
case Qt::Key_Plus: // 增加采样数(提高图像质量)
samplesPerPixel = std::min(samplesPerPixel * 2, 64);
qDebug() << "Samples per pixel:" << samplesPerPixel;
render();
return;
case Qt::Key_Minus: // 减少采样数(提高渲染速度)
samplesPerPixel = std::max(samplesPerPixel / 2, 1);
qDebug() << "Samples per pixel:" << samplesPerPixel;
render();
return;
case Qt::Key_R: // 重新渲染
render();
return;
}
if (needUpdate) {
render(); // 重新渲染场景
update(); // 更新显示
qDebug() << "update";
}
}
// 窗口大小调整事件处理
void resizeEvent(QResizeEvent* event) override {
QWidget::resizeEvent(event);
image = QImage(width(), height(), QImage::Format_RGB32); // 重新创建图像
render(); // 重新渲染
}
};
int main(int argc, char* argv[]) {
QApplication app(argc, argv);
ImageWidget widget;
widget.setWindowTitle("光线追踪渲染器");
widget.show();
return app.exec();
}
#include "main.moc"最后渲染出来的结果如图所示: